Consider the function f ( z) = z 2 Prove that level curves of R e ( f ( z)) and I m ( f ( z)) at z = 1 2 i are orthogonal to each other I am not sure how to apply level curves or contour lines for complex variables As far as real variables go, I am aware that for a function like f ( x, y) = x 2 y 2, the level curves are the circlesDefine the level curves of a function of two variables Describe how level curves can help you sketch a graph of a surface Give examples of several surfaces whose level curves are circles and at least one example of a surface whose level curves are not circles Please explain with wordsFunctions of two variables can be described numerically (a table), graphically, algebraically (a formula), or in English are connected with curves Each particular output is called a level, and these curves are called level curves or contours The closer the curves are to each other, the steeper that section of the surface Topographical
2
Level curves of a function of two variables
Level curves of a function of two variables-Level curves The two main ways to visualize functions of two variables is via graphs and level curves Both were introduced in an earlier learning module Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = c Notice the critical difference between a level curve CDefinition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f ) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f has height k




11 Level Curves And Contour Lines Of Functions Of Two Variables Youtube
The graph itself is drawn in an ( x, y, z) coordinate system Remark 2 Level curves of the same function with different values cannot intersect Remark 3 Level curves of utility functions are called indifference curvesSay for example I give you a function of two variables $z = f(x,y)$ = $x^2 y^2$ which represents a paraboloid If I want the level curves $f(x,y) = c$, then these now represent concentric circles in the $xy$ plane centered at the origin of radius $\sqrt{c}$Level Curves and Contour Maps The level curves of a function f(x;y) of two variables are the curves with equations f(x;y) = k, where kis a constant (in the range of f) A graph consisting of several level curves is called a contour map Level Surfaces The level surfaces of a function f(x;y;z) of three variables are the surfaces
A level curve of a function of two variables is completely analogous to a contour line on a topographical map (a) A topographical map of Devil's Tower, Wyoming Lines that are close together indicate very steep terrainRemark 1 Level curves of a function of two variables can be drawn in an ( x, y) coordinate system; §151 FUNCTIONS OF TWO OR MORE VARIABLES §151 Functions of Two or More Variables After completing this section, students should be able to • Match equations of the form z = f(x,y) to graphs of surfaces and graphs of level curves • Describe the graphs of functions of three variables w = f(x,y,z) in terms of the level curves f(x,y,z) = k 124 You need to be able to
Transcribed image text (3 points) Writing Prompt 1 (typed 1000 words) In your own words, define the level curves of a function of two variables Describe how level curves can help you sketch a graph of a surface Give examples of several surfaces whose level curves are circles and at least one example of a surface whose level curves are not circles f (x,y,z) = 1 x2 y2 4z f ( x, y, z) = 1 x 2 y 2 4 z Solution f (x,y) = 1 x √y 4 −√x1 f ( x, y) = 1 x y 4 − x 1 Solution For problems 5 – 7 identify and sketch the level curves (or contours) for the given function 2x−3y z2 =1 2 x − 3 y z 2 = 1 Solution 4z2y2−x =0 4 z 2 y 2 − x = 0 SolutionA function of two variables is a surface drawn in 3 dimensions;




Lecture Notes Chapter 1 1 Part2 Contourlines Level Curves And 3d Graphs Pdf



A Simple Explanation Of Why Lagrange Multipliers Works By Andrew Chamberlain Ph D Medium
• Estimating partial derivatives from level curves Limits of functions with two variables In studying functions of one variable we used one and twosided limits We cannot talk of twosided or onesided limits of functions of two variables Instead we find limits by studying the values of functions along paths, as in the next definition†When we talk about the graph of a function with two variables defined on a subset D of the xyplane, we mean zfxy xy D= (, ) ,( )∈ If c is a value in the range of f then we can sketch the curve f(x,y) = cThis is called a level curve A collection of level curves can give a good representation of the 3d graph Plot an equation containing two variables in C# This example uses the same techniques to plot level curves For a function z = F(x, y), the program simply plots the function F(x, y) – z = 0 for different z values This example makes curves red when z < 0, blue when z > 0, and black when z = 0




11 Level Curves And Contour Lines Of Functions Of Two Variables Youtube



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id
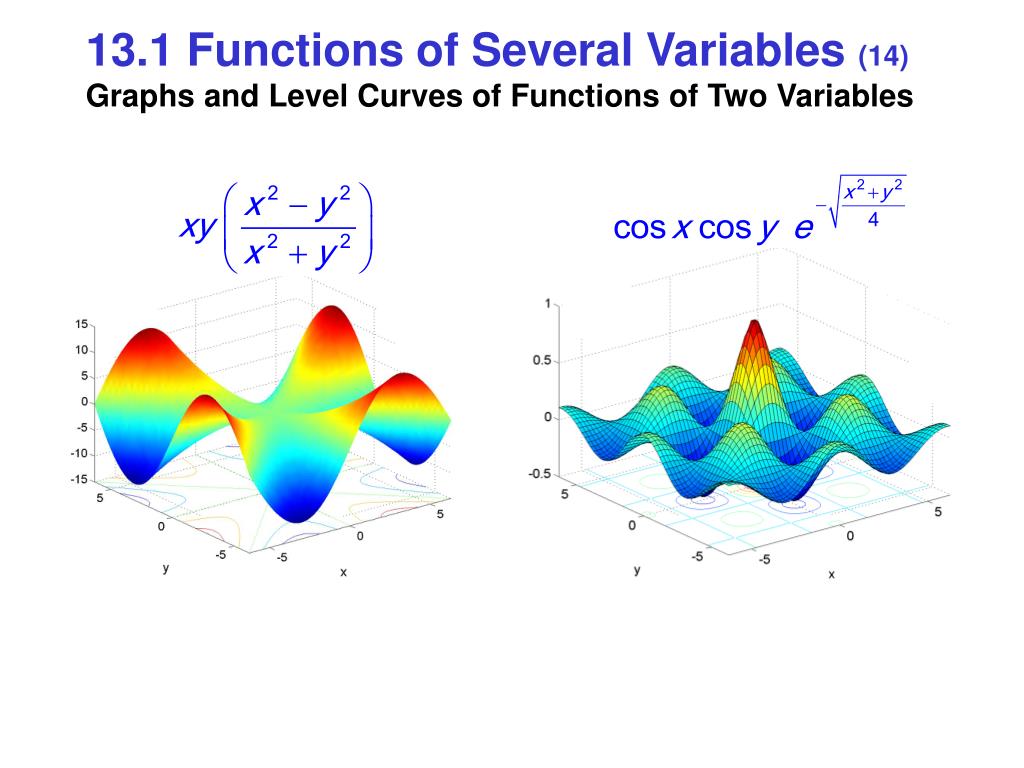
Define the level curves of a function of two variables Describe how level curves can help you sketch a graph of a surface Give examples of several surfaces whose level curves are circles and at least one example of a surface whose level curves are not circles Math Calculus MATH 2110QOne way to study the graph z = f(x,y) of a function of two variables is to study the graphs of the functions of one variable that are obtained by holding x or y constant To understand this process, we need to look at the geometric significance of setting x or y equal to a constantLevel Curves and Surfaces The graph of a function of two variables is a surface in space Pieces of graphs can be plotted with Maple using the command plot3d For example, to plot the portion of the graph of the function f (x,y)=x 2 y 2 corresponding to x between 2 and 2 and y between 2 and 2, type > with (plots);



2




Level Curves Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
That is, a set where the function takes on a given constant value c When the number of variables is two, a level set is generically a curve, called a level curve, contour line, or isoline So a level curve is the set of all realvalued solutions of an equation in two variables x 1 and x 2A function of three variables is a hypersurface drawn in 4 dimensions Question define the level curves of a function of two variables Describe how level curves can help you sketch a graph of a surface Give examples of several surfaces whose level curves are circles and at least one example of a surface whose level curves are not circles Please explain with words



Math Tutor Extra Functions Of More Variables




Calculus Iii Functions Of Several Variables
A level curves of a function 11eaa8b1_d9f0_b4f4_b1b6_77fbf6bf60f1_TB6026_11 of two variables, 11eaa8b1_d9f0_b4f5_b1b6_9bc2d_TB6026_11 , A) Exists for all values of 11eaa8b1_d9f0_dc06_b1b6_e5d58ec0521e_TB6026_11 B) Exists for all values of 11eaa8b1_d9f1_0317_b1b6_2ff5a7a97e19_TB6026_11 C) Exists for all values ofFor a function of three variables, one technique we can use is to graph the level surfaces, our threedimensional analogs of level curves in two dimensions Given , the level surface at is the surface in space formed by all points whereA level curve (or contour) of a function f of two independent variables x and y is a curve of the form k = f (x, y), where k is a constant Topographical maps can be used to create a threedimensional surface from the twodimensional contours or level curves




Ppt Functions Of Several Variables Partial Derivatives Powerpoint Presentation Id



13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned
Example 72 Suppose we want to describe the elevation above see level of each point on the surface of a mountain For simplicity, suppose that the mountain just looks like a cone, with the base at sea level The altitude can be represented by the function \\begin{eqnarray*} fD & \longrightarrow & {\mathbb R} \\ z & = & f(x,y), \end{eqnarray*}\ associating to each point in theChapter 2 Surfaces and Curves Section 21 Functions, level surfaces, quadrics A function of two variables f(x,y) is usually defined for all points (x,y) in the plane like in the example f(x,y) = x2 sin(xy) In general, we need to restrict the function to a doLevel curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constant For example the curve at height z = 1 is the circle x2 y2 = 1 On the graph we have




Document




13 1 Functions Of Several Variables Mathematics Libretexts
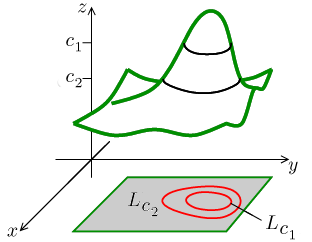
So level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplane And if we're being careful and if we take the convention that our level curves are evenly spaced in the zplane, then these are going to get closer and closer together, and we'll see in a minute where that's coming from So let's draw what's going on in three dimensionsWhere c=constant If f= height, level curves are contours on a contour map If f= air pressureLevel Curves The level curves f (x, y) = k are just the traces of the graph of f in the horizontal plane z = k projected down to the xyplane So if you draw the level curves of a function and visualize them being lifted up to the surface at the indicated height, then you can mentally piece together a picture of the graph




Solved 15 1 Graphs And Level Curves 927 A Figure 15 18 Chegg Com




14 Partial Derivatives Partial Derivatives So Far We
It looks much like a topographic map of the surface In figure 1412 both the surface and its associated level curves are shown Note that, as with a topographic map, the heights(1) We can write the surface as a level surface f(x, y, z) = c of a function of three variables, f(x, y, z) (2) We can parameterize the surface by writing x, y, and z each as functions of two parameters, say s and t This is analogous to parameterizing a curve and writing x, y, and zBe able to describe and sketch the domain of a function of two or more variables Know how to evaluate a function of two or more variables Be able to compute and sketch level curves & surfaces PRACTICE PROBLEMS 1 For each of the following functions, describe the domain in words Whenever possible, draw a sketch of the domain as well (a) f



1




Functions Of Two Variables Graph Of A Function
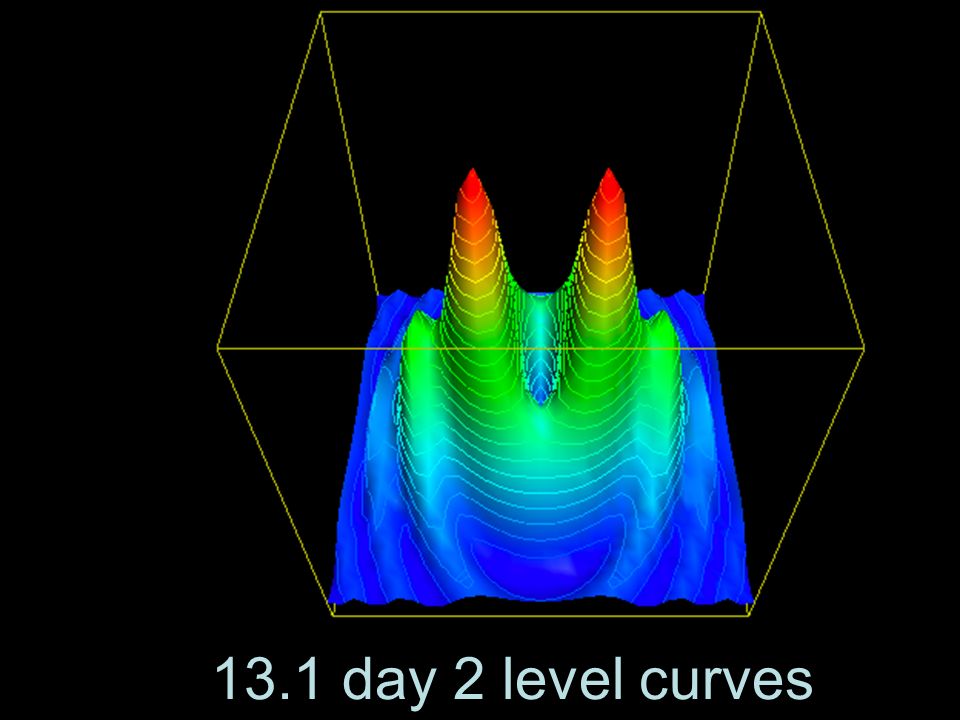
Level Surfaces It is very difficult to produce a meaningful graph of a function of three variables A function of one variable is a curve drawn in 2 dimensions;19 Level Curves A second way to visualize a function of two variables is to use a scalar field in which the scalar z = f(x, y) is assigned to the point (x, y)A scalar field can be characterized by level curves (or contour lines) along which the value of f(x, y) is constant For instance, the weather map112 Contours and level curves Three dimensional surfaces can be depicted in two–dimensions by means of level curves or contour maps If f DˆR2!R is a function of two variables, the level curves of f are the subsets of D f(x;y) 2D f(x;y) = cg;




Chapter 14 Partial Derivatives Chapter 14 Partial Derivatives Ppt Download




Level Curves And Implicit Differentiation Studocu
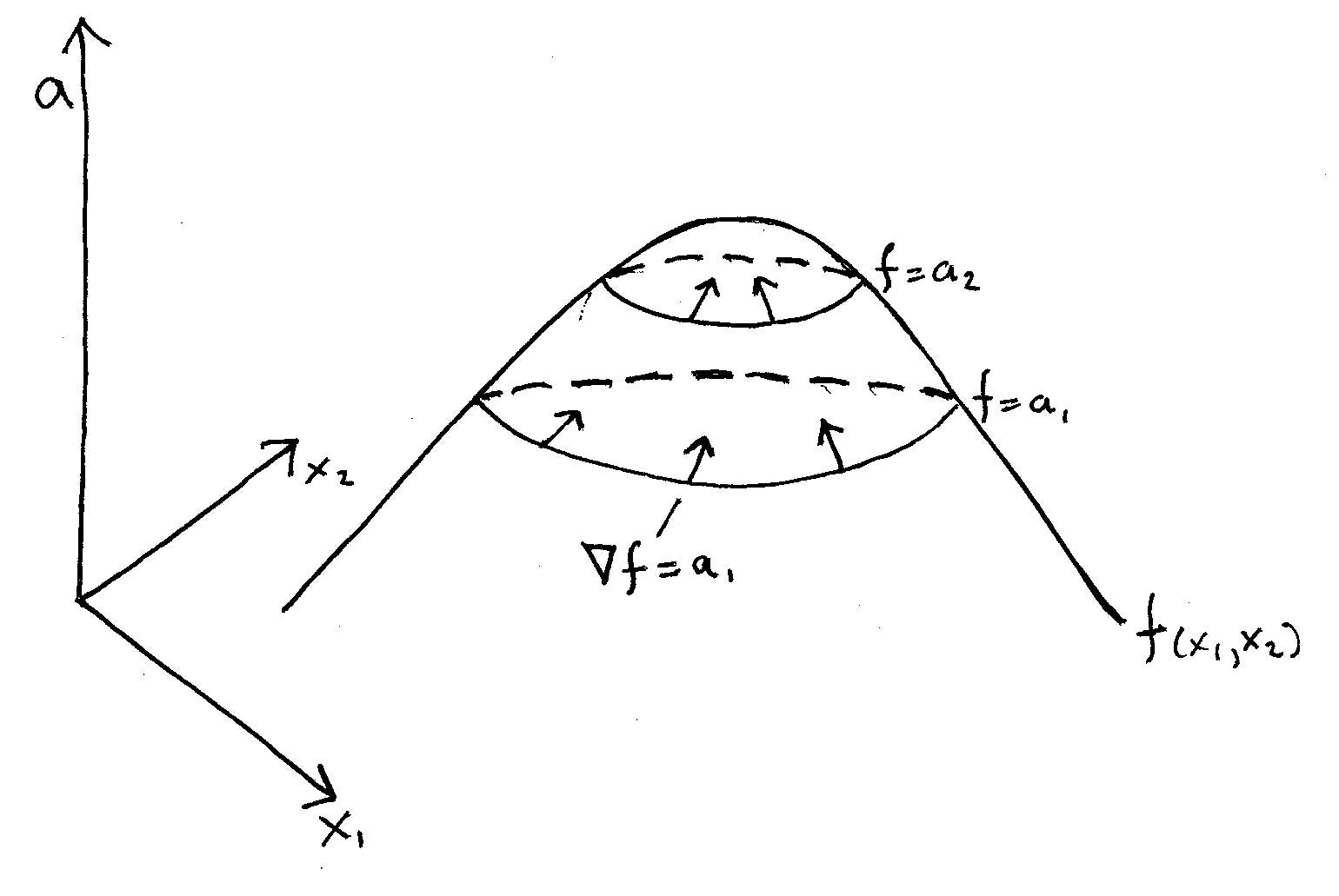
What we want to be able to do is slice through the figure at all different heights in order to get what we call the "level curves" of a function Then we want to be able to transfer all those twodimensional curves into the twodimensional plane, sketching those in the xyplane This will give us the sketch of level curves of the functionC Graph the level curve AHe, iL=3, and describe the relationship between e and i in this case T 37 Electric potential function The electric potential function for two positive charges, one at H0, 1L with twice the strength as the charge at H0, 1L, is given by fHx, yL= 2 x2 Hy1L2 1 x2 Hy 1L2 a Graph the electric potential using the window @5, 5Dµ@5, 5Dµ@0, 10 D If the intersection is a curve or isolated points, that is called the "level set" or "level curve" of function Here, we use the graph of and have set two different zlevels in red, in blue The intersections are circles in space called "level curves"




How To Sketch Graphs For Functions Of Two Variables Chris Tisdell Unsw Youtube
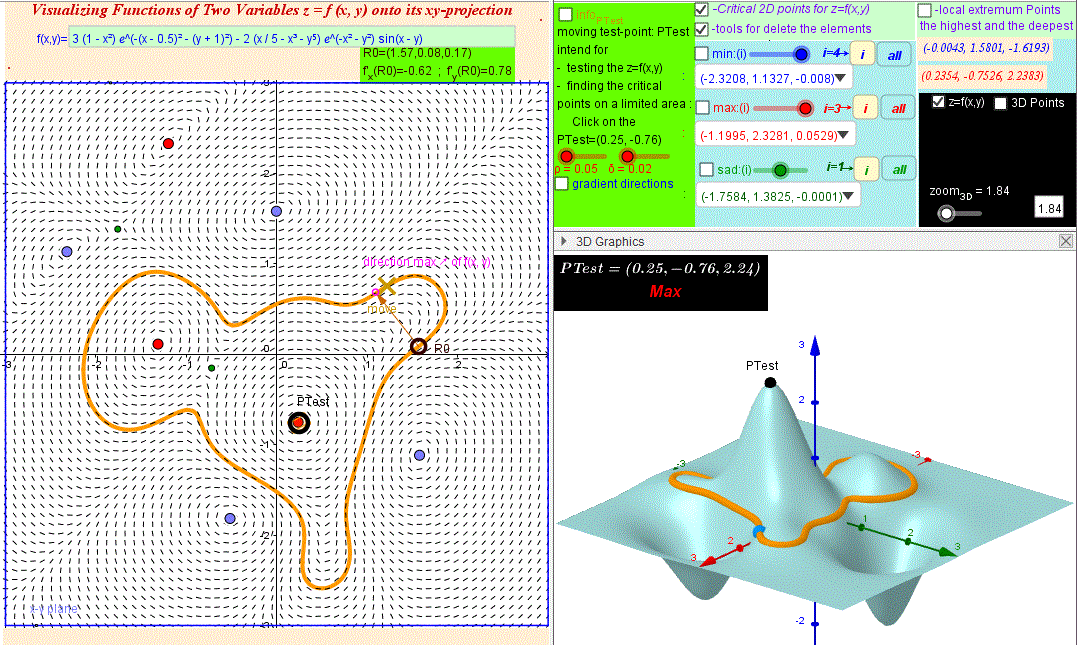



Visualizing Functions Of Two Variables Geogebra
Multivariable Functions Domains Ranges Graphs Level Curves A function of two variables z = (x, y) maps each ordered pair (x, y) in a subset d of the real plane ir2 to a unique real number z the set d is called the domain of the function the range of f is the set of all real numbers z that has at least one ordered pair (x, y) ∈ d such that f(x, y) = z as shown in figure 221I Functions of two variables I Graph of the function I Level curves, contour curves I Functions of three variables I Level surfaces On open and closed sets in Rn We first generalize from R3 to Rn the definition of a ball of radius r centered at Pˆ Definition A set B r (Pˆ) ⊂ Rn, with n ∈ N and r > 0, is a ball of radius r The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equations of the level curves are \(f\left( {x,y} \right) = k\) Note that sometimes the equation will be in the form \(f\left( {x,y,z} \right) = 0\) and in these cases the equations of the level curves are \(f\left( {x,y,k} \right) = 0\)




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
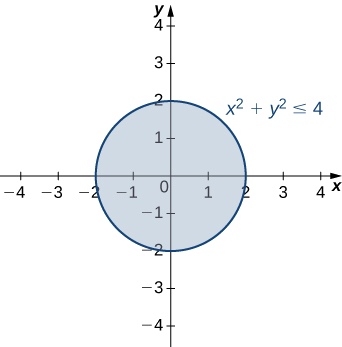



13 1 Functions Of Multiple Variables Mathematics Libretexts
LEVEL CURVES 2D If f(x;y) is a function of two variables, then f(x;y) = c = constis a curve or a collection of curves in the plane It is called contour curve or level curve For example, f(x;y) = 4x2 3y2 = 1 is an ellipse Level curves allow to visualize functions of two variables f(x;y) LEVEL SURFACES We will later see also 3D anaMATH 1 Multivariable Calculus at Queens College, Spring 21We are following Stewart's Essential CalculusX y 143 Level Curves and Level Surfaces Look over book examples!!!



2




Ppt Chapter 14 Partial Derivatives Powerpoint Presentation Free Download Id
As in this example, the points $(x,y)$ such that $f(x,y)=k$ usually form a curve, called a level curve of the function A graph of some level curves can give a good idea of the shape of the surface; a level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of function when equated to some constant values ,example a function of two variables say x and y ,then level curve is the curve of points (x,y) ,where function have constant value can be better understood by an Level Curves and Surfaces Example 2 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surface such that every tangent plane to the surface at a point of the set is parallel to the level set




Introduction To Functions Of Several Variables Ppt Download
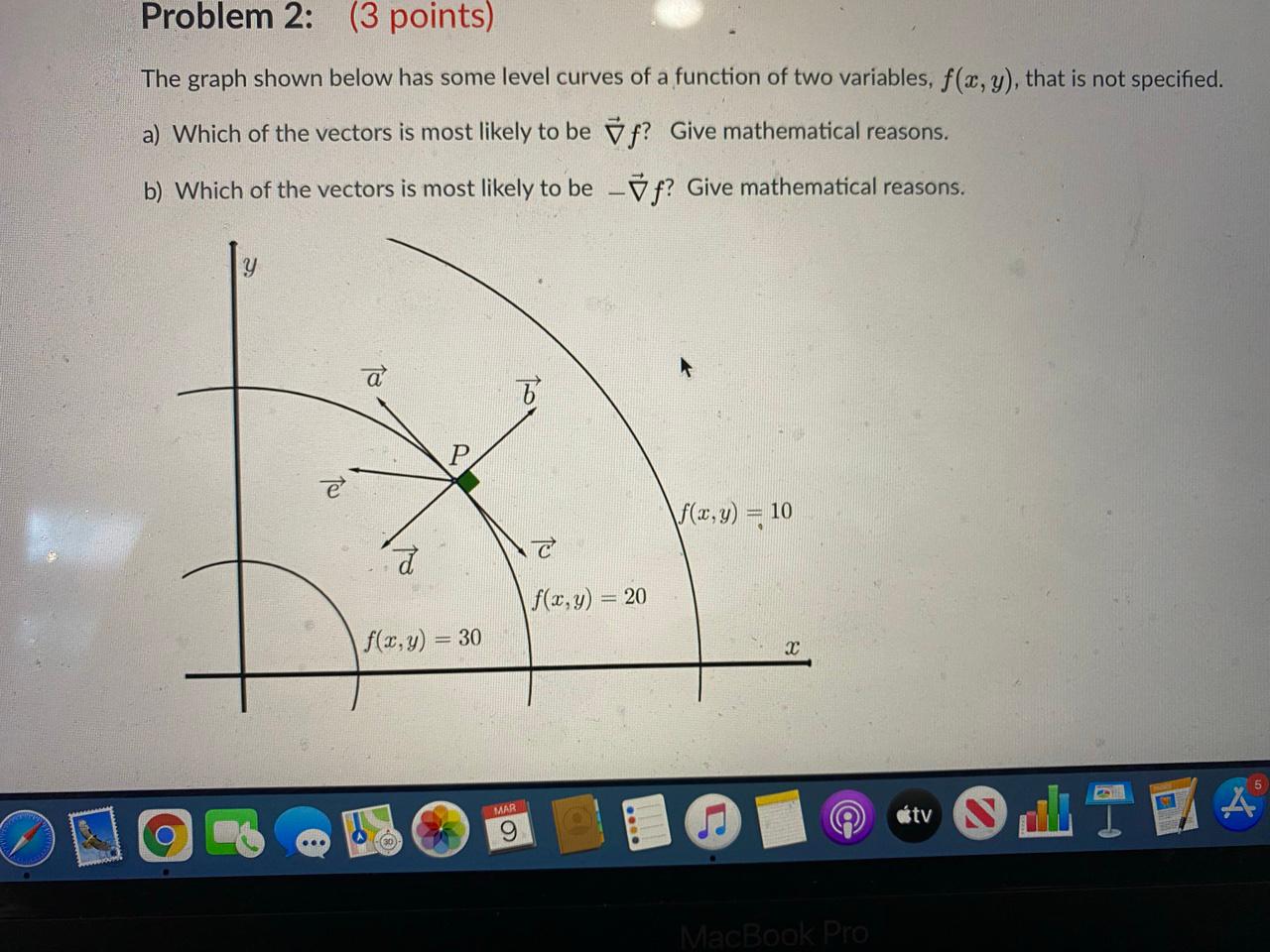



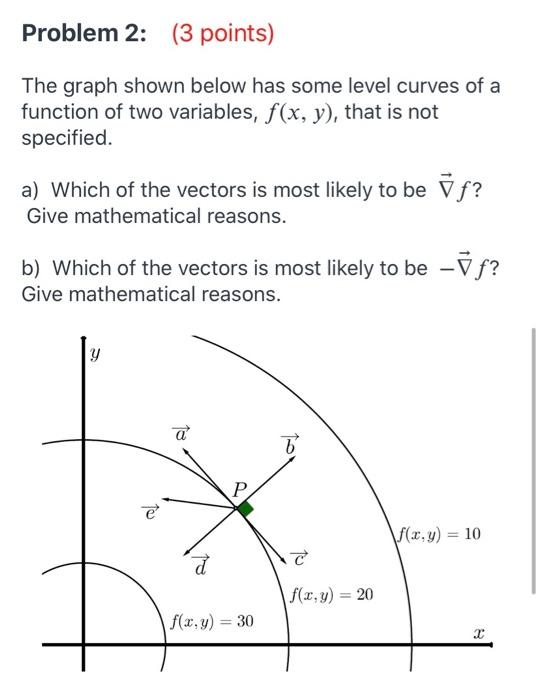
Solved Problem 2 3 Points The Graph Shown Below Has Some Chegg Com
With a function of two variables, each ordered pair ( x, y) in the domain of the function is mapped to a real number z Therefore, the graph of the function f consists of ordered triples ( x, y, z) The graph of a function z = ( x, y) of two variables is called a surfaceLevel Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the corresponding curves on the surface, the intersection of the surface with the plane z = k



0 3 Visualizing Functions Of Several Variables
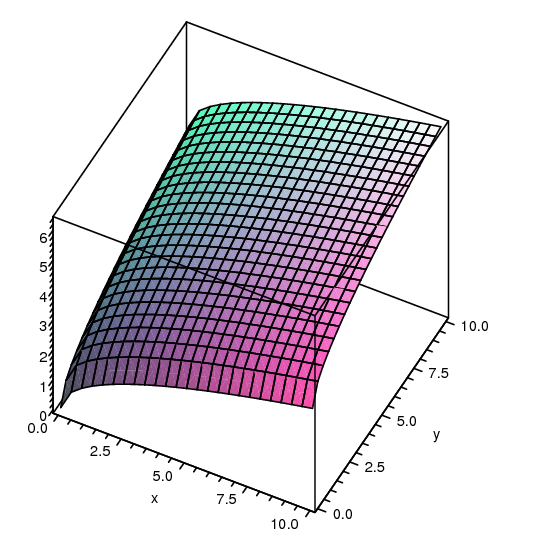



16 1 Functions Of Several Variables




Document



1




Level Curves




Level Curves R Calculus
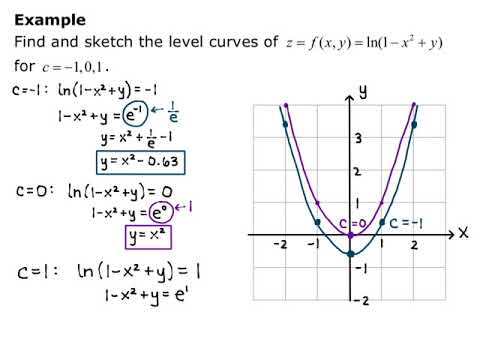



Section 13 1 Level Curves Youtube
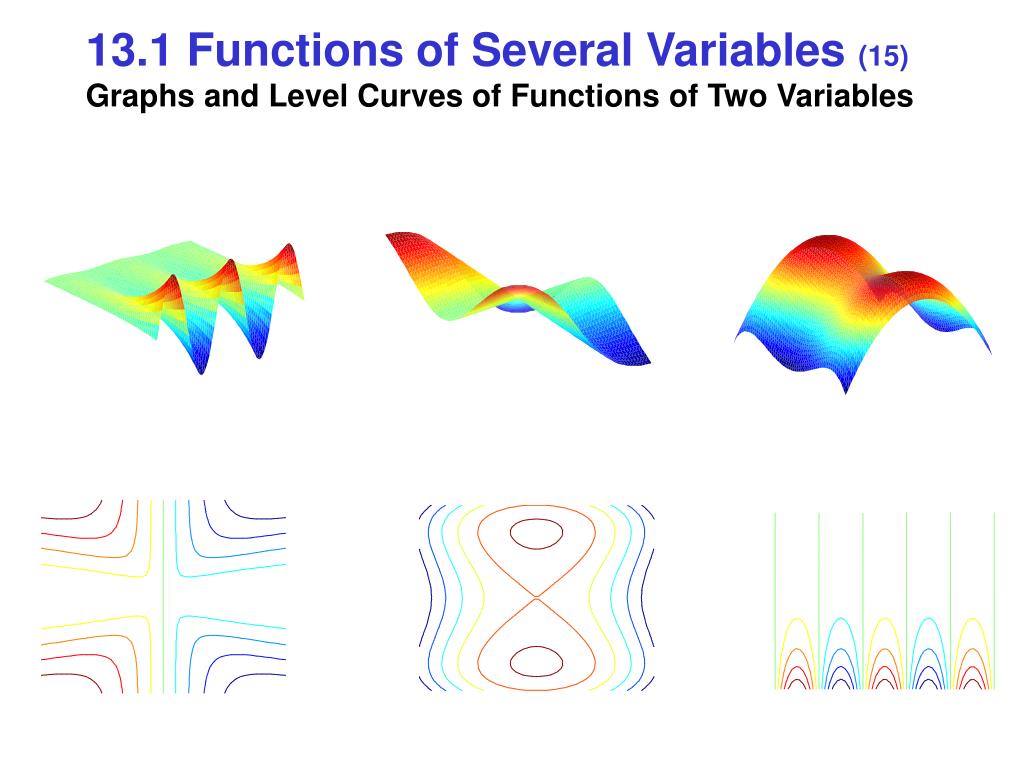



Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id



Business Calculus




Solved Given Two Variables Function 4x2 Y2 2 Determine The Domain And Range For The Function Cot Po1 2 Marks Sketch The Contour Iines For Level Curves K 2 3 The Xz Trace And Yz Trace




Graphs Of Functions Of Two Variables




Sketch Saddle Point Of A Function Of Two Variables F X Y 4 X 3 Y 3 3xy Stewart P930 Question 14 7 3 Mathematics Stack Exchange
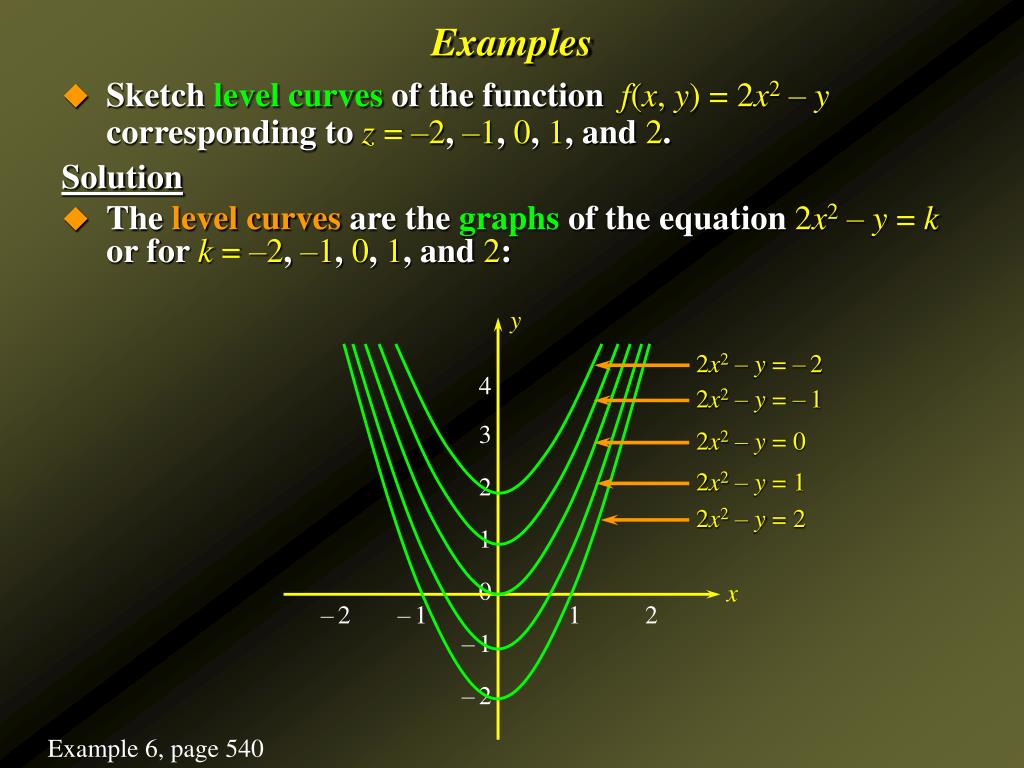



Ppt Functions Of Several Variables Partial Derivatives Powerpoint Presentation Id




How To Sketch Level Curves Youtube



Ocw Nctu Edu Tw




Functions Of Several Variables




How To Find The Level Curves Of A Function Calculus 3 Youtube




Level Curves
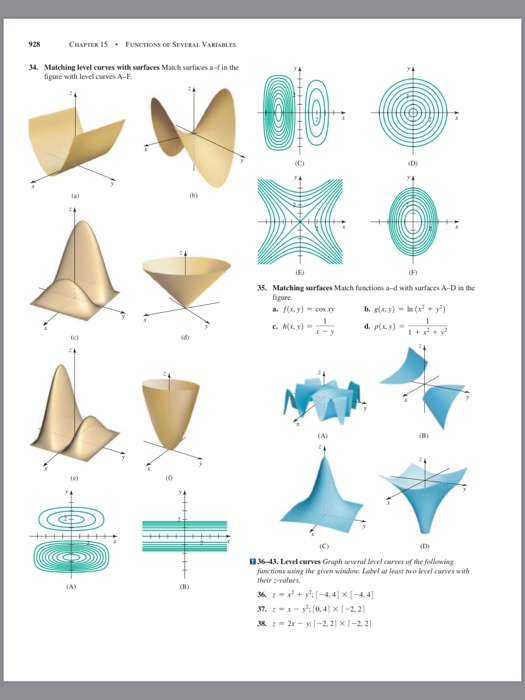



Solved 15 1 Graphs And Level Curves 927 A Figure 15 18 Chegg Com



2



Solved Problem 2 3 Points The Graph Shown Below Has Some Chegg Com




Level Curves



Functions Of Two Variables Lessons Blendspace



2



Calculus Iii Functions Of Several Variables




Level Sets Math Insight



Function Of Several Variables Several Level Curves Geogebra
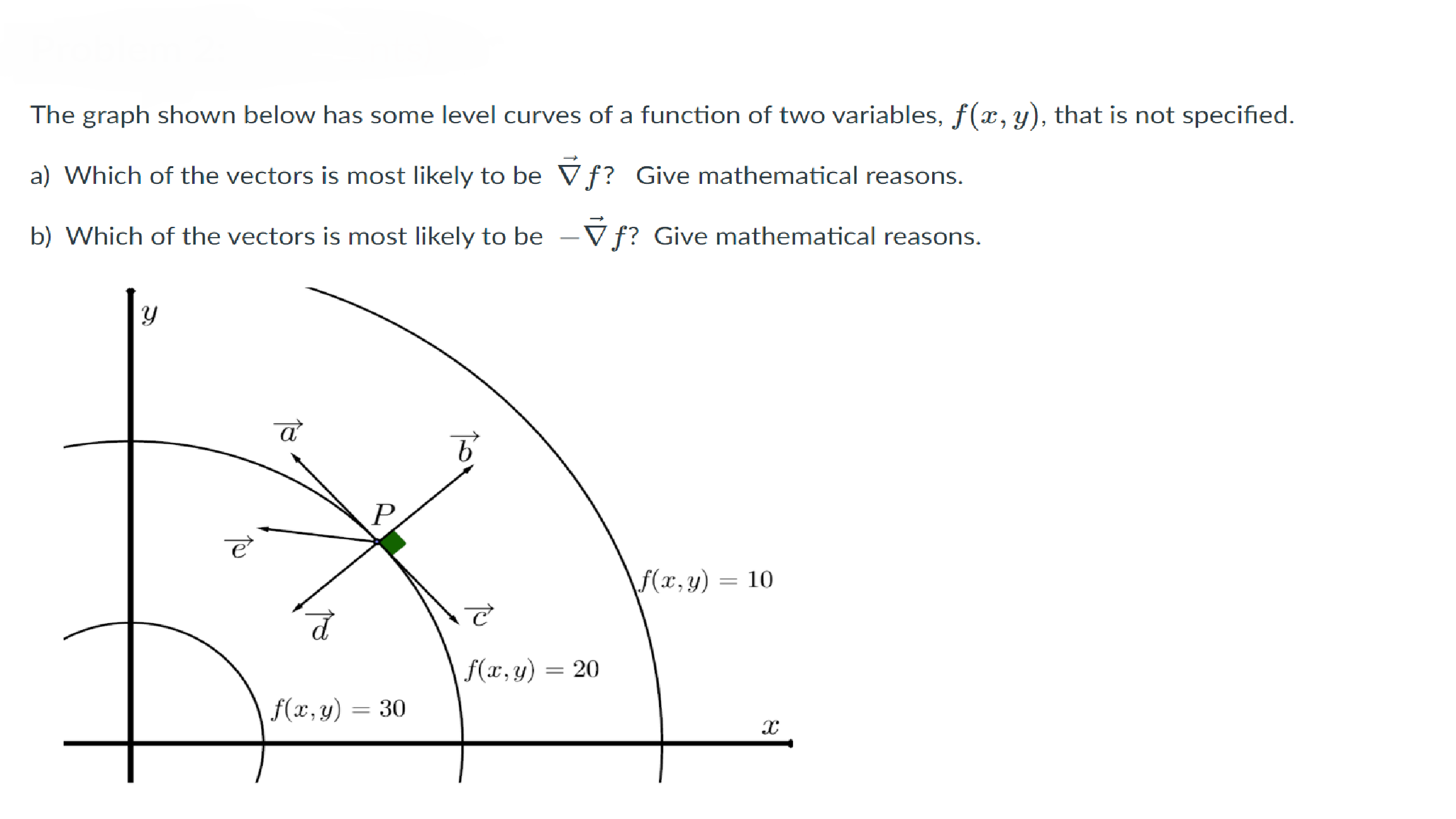



Solved The Graph Shown Below Has Some Level Curves Of A Chegg Com



1
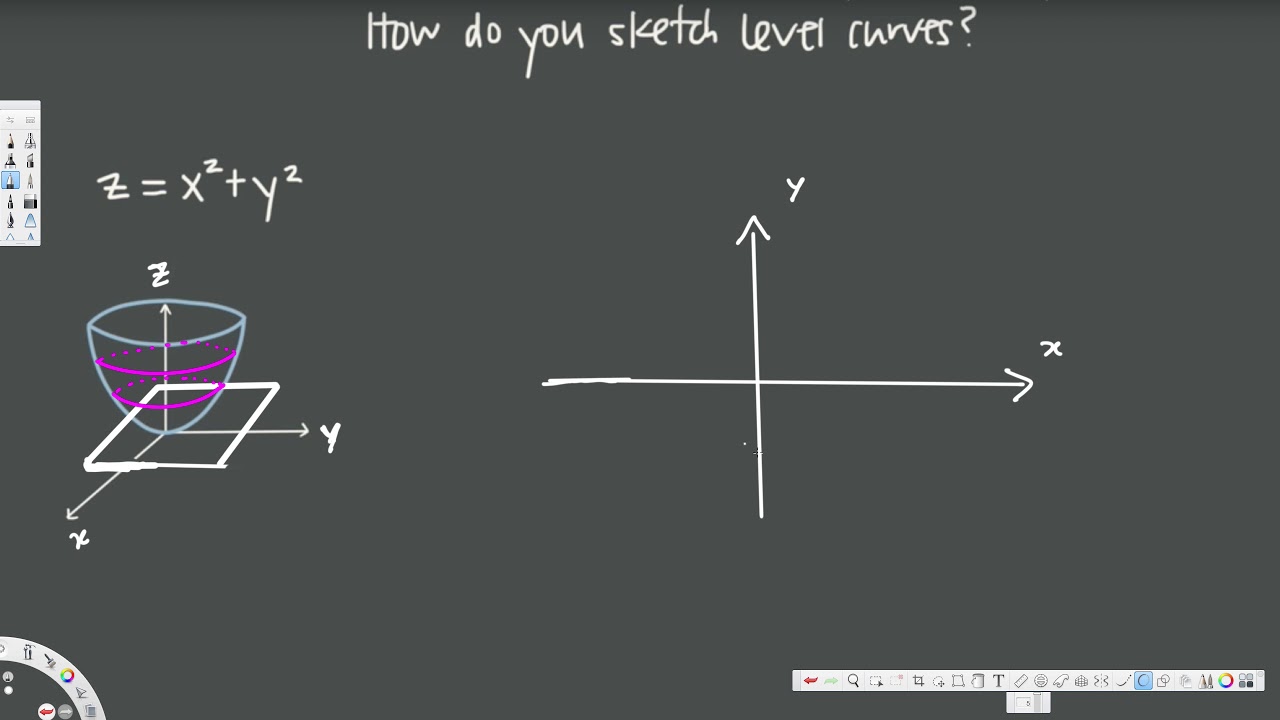



How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 1 Youtube



Business Calculus



1
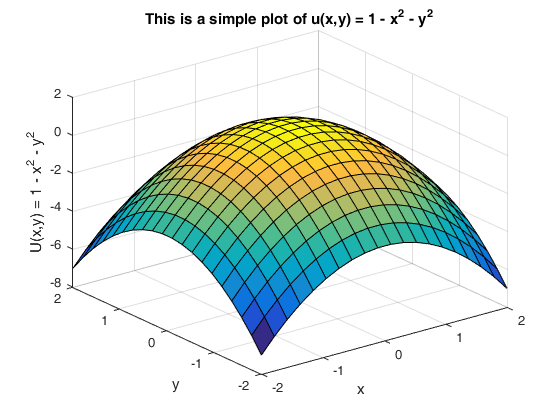



Howtoplotfunctiontwovariables




Solved Points Writing Prompt Typed 100 0 Words Eyouitown Words Define The Level Curves Of A Function Of Two Variables Describe How Level Curves Can Help You Sketch A Graph Of A Surfacea Examples




13 1 Introduction To Multivariable Functions Chapter 13 Functions Of Several Variables Calculus Iii




Announcements Topics To Do Ppt Download




Level Sets Math Insight
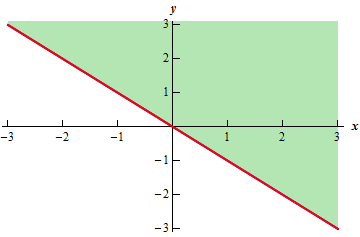



Calculus Iii Functions Of Several Variables



Functions Of Several Variables Ximera




Level Sets Math Insight



Solved Define The Level Curves Of A Function Of Two Variables Give Examples Of Several Surfaces Whose Level Curves Are Circles And At Least One Ex Course Hero
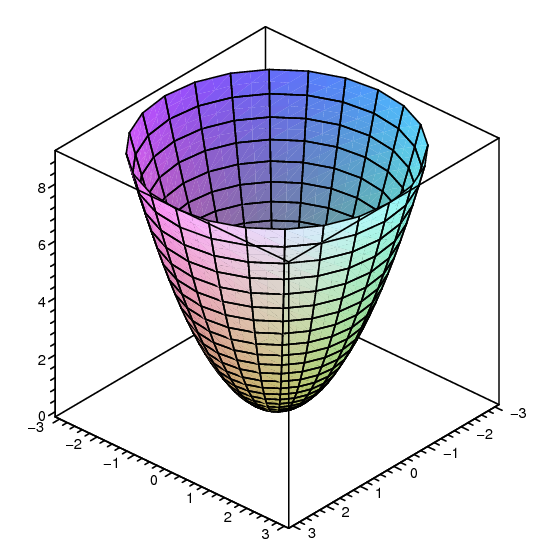



16 1 Functions Of Several Variables
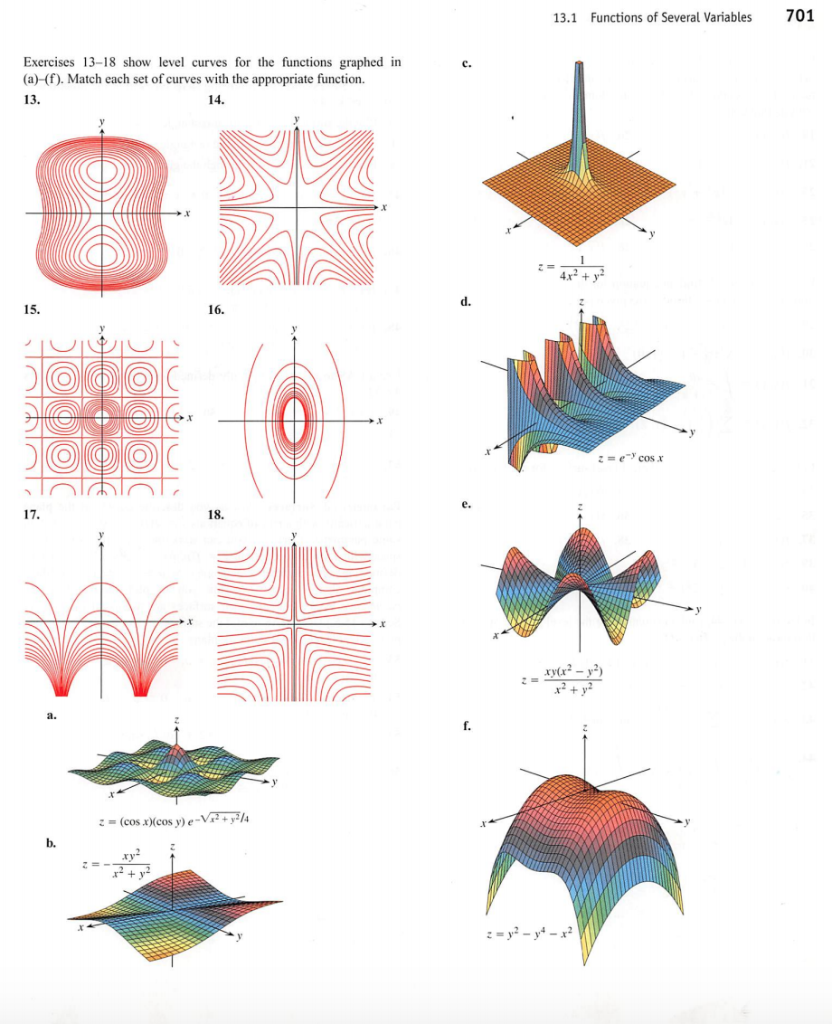



Solved 13 Functions Of Several Variables 701 Exercises Chegg Com




14 Partial Derivatives Copyright Cengage Learning All Rights




Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram



2




Functions Of Several Variables




16 1 Functions Of Several Variables



Calculus Iii Functions Of Several Variables




Calculus Iii Functions Of Several Variables



The Gradient And Directional Derivative




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



13 1 Functions Of Several Variables Mathematics Libretexts




Calculus Iii Functions Of Several Variables



Level Sets Math Insight
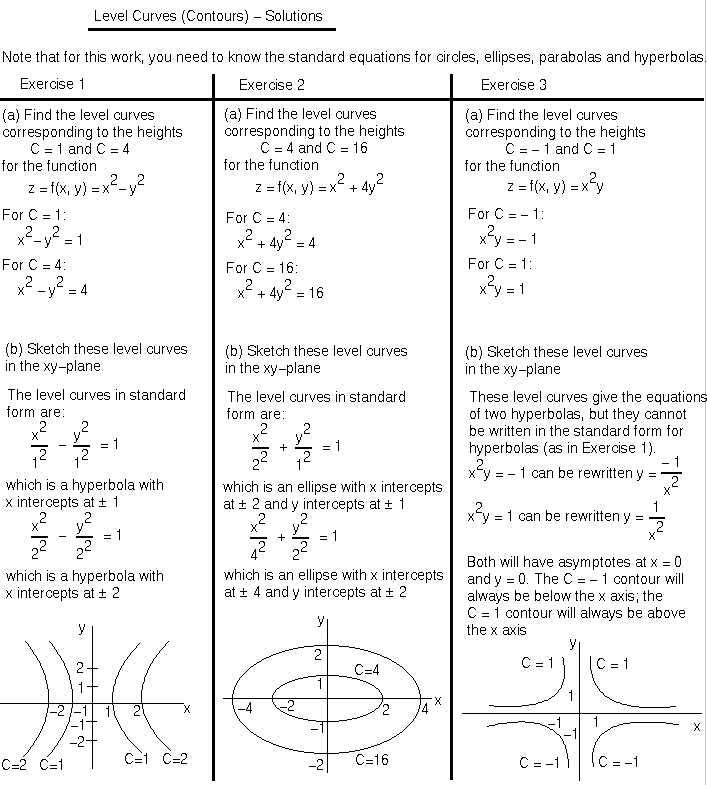



Functions Of Two Variables Math100 Revision Exercises Resources Mathematics And Statistics University Of Canterbury New Zealand




Calculus Iii Functions Of Several Variables
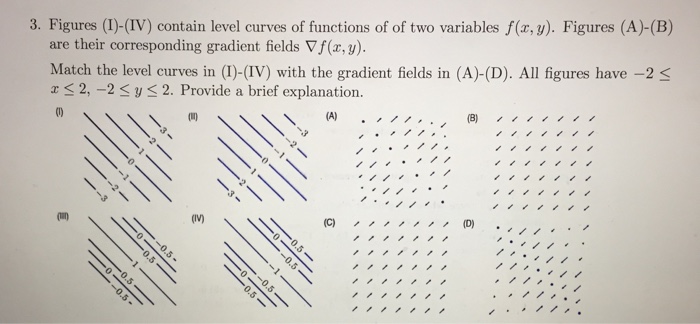



Solved Figures I Iv Contain Level Curves Of Functions Of Chegg Com
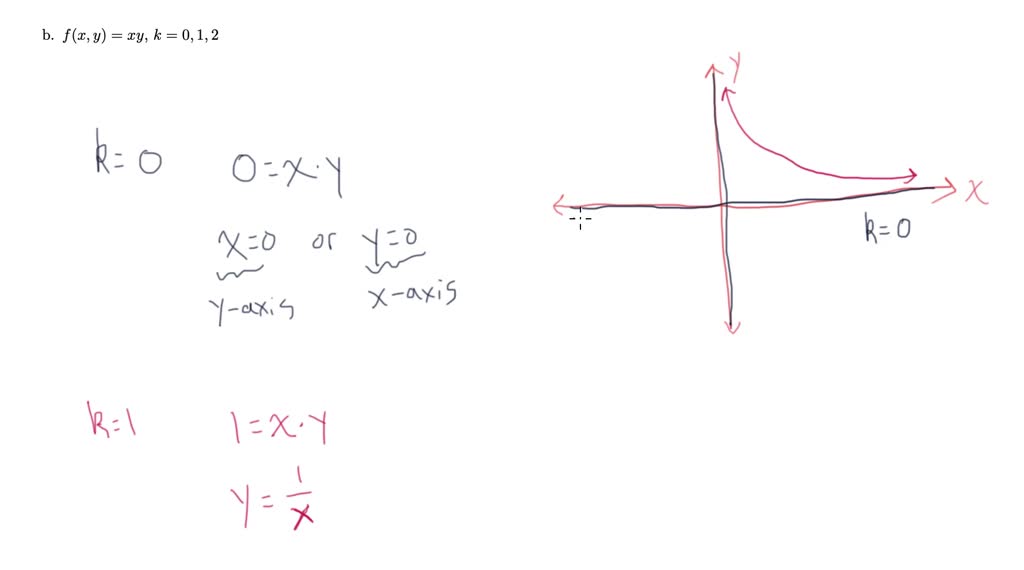



Level Curves And Surfaces Example 2 Numerade




Functions Of Two And Three Variables Level Curves Contours Level Surfaces Youtube
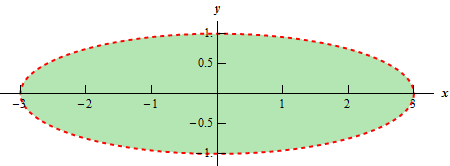



Calculus Iii Functions Of Several Variables



0 3 Visualizing Functions Of Several Variables



Functions Of Several Variables



0 3 Visualizing Functions Of Several Variables
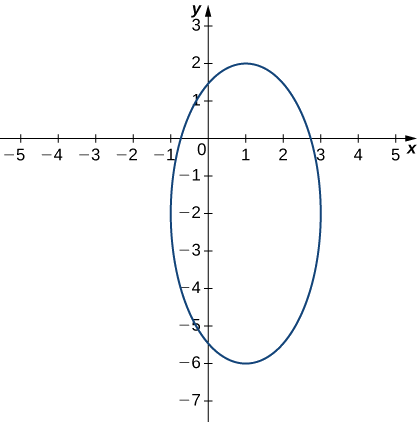



13 1 Functions Of Several Variables Mathematics Libretexts



0 3 Visualizing Functions Of Several Variables



2



Business Calculus



Functions Of Several Variables Ximera



Draw Level Curves For Functions Of Two Variables In C C Helper




Ppt Multivariable Functions Of Several Their Derivatives Powerpoint Presentation Id




Level Curves




Level Set Wikipedia




Level Curves Of Functions Of Two Variables Youtube
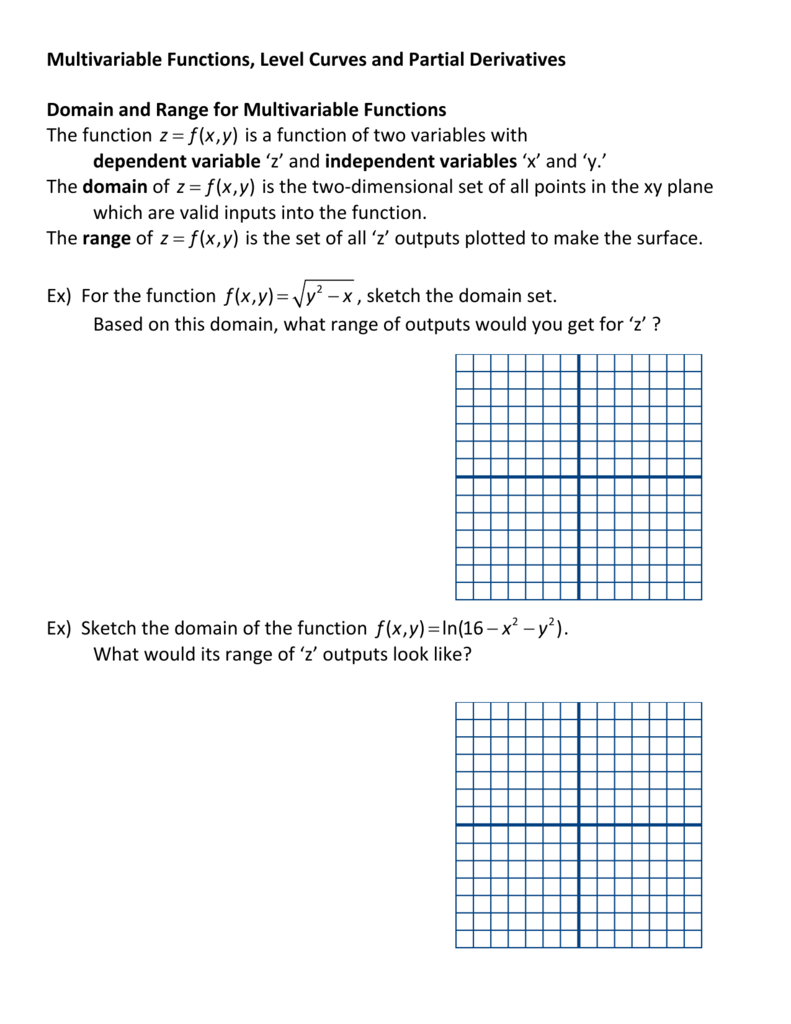



Multivariable Functions Level Curves And Partial Derivatives




Solved 1 Describe The Level Curves Of The Function Z 2x2 Chegg Com




Level Set Wikipedia
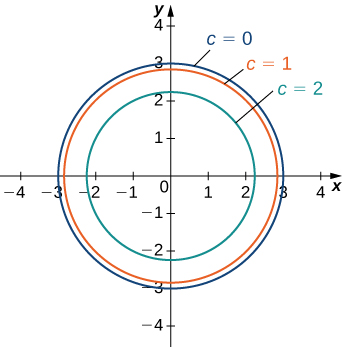



13 1 Functions Of Multiple Variables Mathematics Libretexts


