4 How does radian measure of an angle compare to the degree measure?2 π radians = 360 ∘ π radians = 360 ∘ 2 = 180 ∘ 1 radian = 180 ∘ π ≈ 573 ∘ 2 π radians = 360 ∘ π radians = 360 ∘ 2 = 180 ∘ 1 radian = 180 ∘ π ≈ 573 ∘ Note that when an angle is described without a specific unit, it refers to radian measureReference Angle and Quadrant Calculator This online calculator finds the reference angle and the quadrant of a trigonometric a angle in standard positionThe reference angle is defined as the acute angle between the terminal side of the given angle and the x axis The given angle may be in degrees or radians
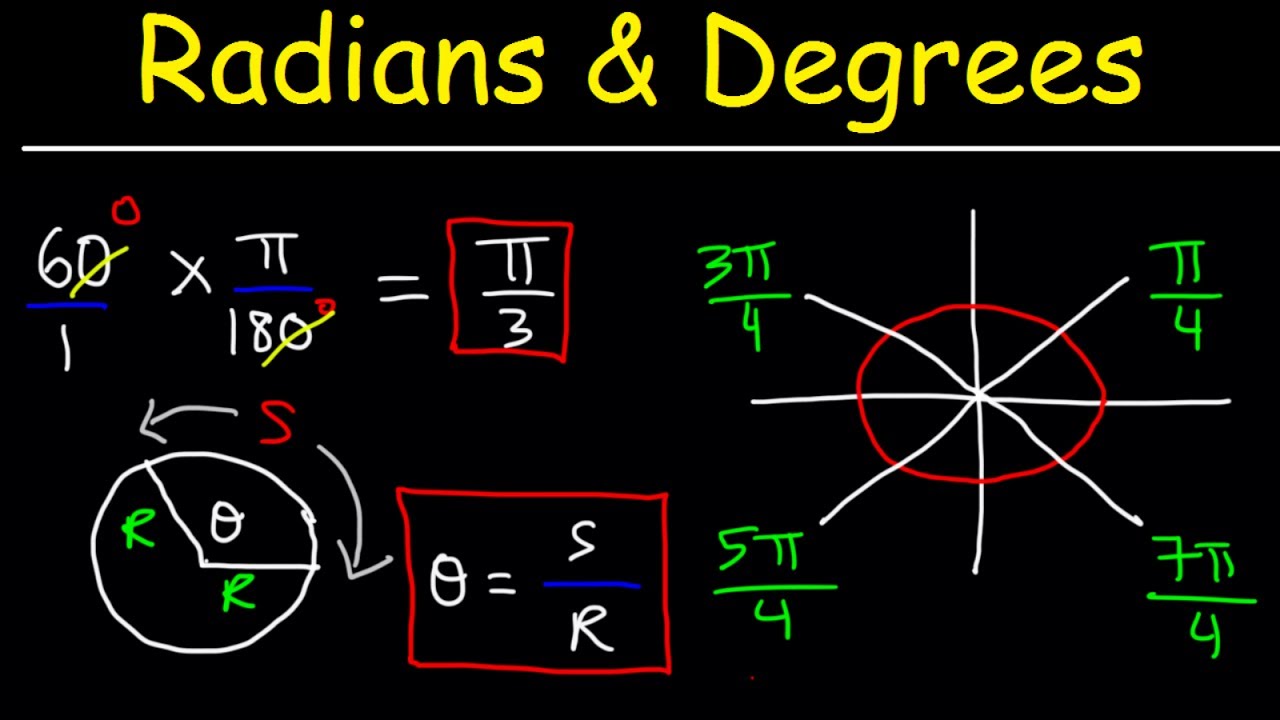
Radians And Degrees Youtube
π 2 radian angle in standard position
π 2 radian angle in standard position-We have a special type of angle in standard position whose terminal side lies on an axis, a quadrantal angle This type of angle can have a measure of 0°, 90°, 180°, 270° or 360° See Figure \(\PageIndex{7}\) Figure \(\PageIndex{7}\) Quadrantal angles are angles in standard position whose terminal side lies along an axisRadian to degree conversion Multiply radians by 180 ° π radian First convert the angle from 15 π 4 radians into degrees using above formula 15 π 4 = 15 π 4 × 180 ° π = 675 ° Now, 675 ° = 360 ° 215 ° The sketch of the angle 15 π 4 in standard position is given below



T1 1d To Find Coterminal Angles Ppt Download
Example 14 Draw the following angles in standard position 5π 2 −135 3 (radians) When changing from degrees to radians or vice versa just remember that degrees/360 is the same fraction of a circle as radians/2π So if an angle is x degrees and y radians, then x 360 = y 2π Solving we have the formulas x = 180 π y and y = πx 180Draw the following angles in standard position 5π 2 −135 3 (radians) When changing from degrees to radians or vice versa just remember that degrees/360 is the same fraction of a circle as radians/2π So if an angle is x degrees and y radians, then x 360 = y 2π Solving we have the formulas x = 180 π y and y = πx 1801 Sketch an angle in standard position of 4 radians 2 Convert the angle measure to radian measure a 78 b 54° 3 The circular blade on a saw has a diameter of 725 inches and rotates at 4800 revolutions per minute Find the angular speed of the blade both in radians per second and as a multiple of π 4
Jan 21, 21 · Draw an angle in standard position with the given measure If the angle measure is not between 0 and 2 π or between 0 ∘ and \ (360^ {\circ\), state the coterminal angle that is within that interval 6) 30 ∘ 7) 300 ∘ 8) − 80 ∘ 9) 135 ∘2 Convert from radians to degrees a) 5 4 π b) 17 6 π c) 7 6 π − d)2radians Coterminal Angles Two angles, when in standard position, have the same terminal angle 3 Find two coterminal angles for the given angle A) 115 ° B) 4 π C) 3 2 π − D) 440 ° Complementary and Supplementary Angles Complementary Angles – The sum of theirThe angles that bisect the other quadrants are π/2 π/4 = 3π/4 radians, π π/4 = 5π/4 radians and 3π/2 π/4 = 7π/4 radians The angle one third of the way through the first quadrant is one twelfth of a revolution, that is, (π/2)/3 = 2π/12 = π/6 radians Double π/6 is twothirds of the way through the first quadrant, or one sixth
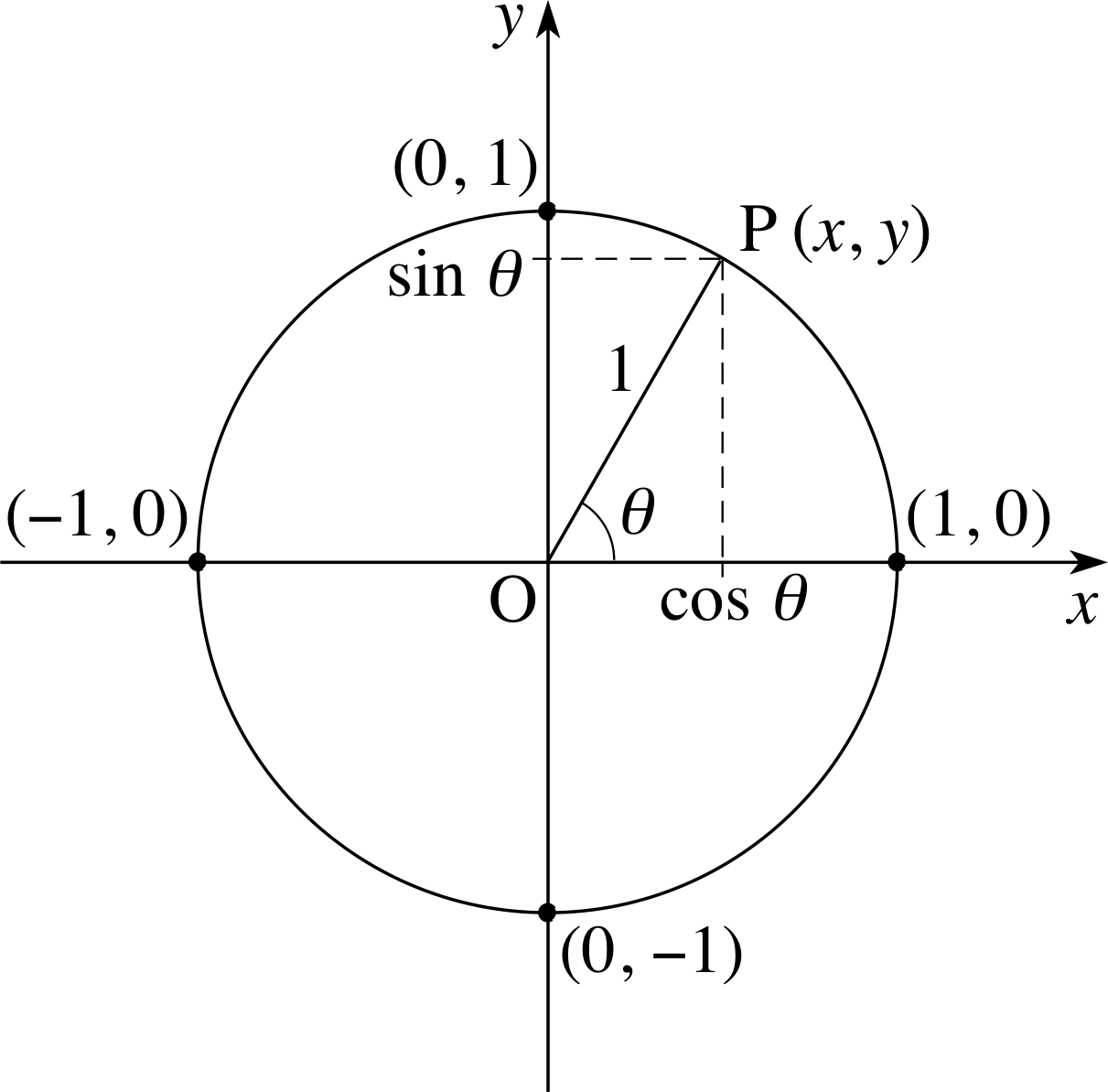
Angles in standard position via radians as well Sketch the following angles on the board (2π, π, π/2, 3π/2 radians) before examining the next example Example Draw and label each angle in standard position (SHOW figure 415 and table 41 on pg 467) θ = α = α = β = θ = Two angles with the same initial and terminal sides (butAug 04, 17 · The terminal side is in the third quadrant pi ~~ 314 so the terminal side of4 is past the negative xaxis (3pi)/2 = 3/2 * pi ~~ 3/2 * 3 = 45 so the terminal side of 4 is not in the fourth quadrant If you want to be a little more precise, note that the pi/4 angle in Quadrant 3 is (5pi)/4 ~~ 15/4 = 375, so the terminal side of 4 is between those of (5pi)/4 and (3pi)/2Recall that the symbol represents the real number constant which is the ratio of the circumference of a circle to its diameter Its value is approximately Since the circumference of the unit circle is 2 it follows that the radian measure of an angle of one revolution is 2The radian measure of an angle whose terminal side is along the negative xaxis is



Angles Precalculus Ii
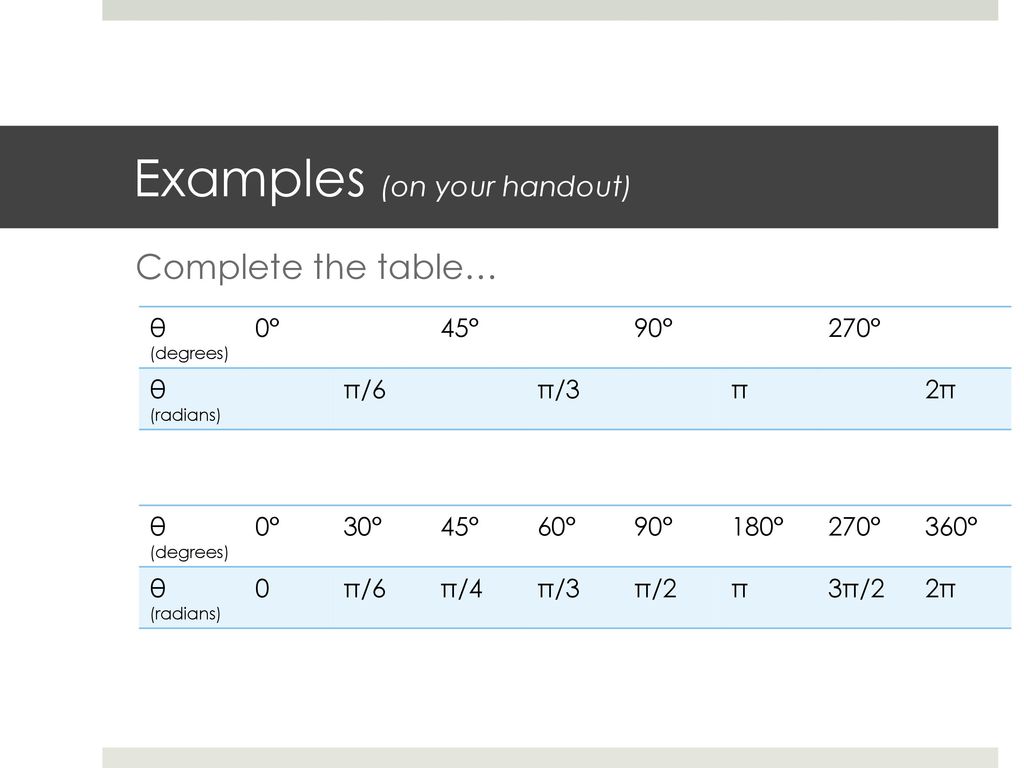


Radian And Degree Measure Ppt Download
This online calculator finds the quadrant of an angle in standard position The given angle may be in degrees or radians Use of calculator to Find the Quadrant of an Angle 1 Enter the angle in Degrees top input example 1250 in Radians second input as a fraction of π Example 27/5 π or 12 πStandard position is when Measure angles in standard position using degree measure and radian measure DRAFT 11th 12th grade 43 times which picture shows an angle of π/6 radians?470 Chapter 9 Trigonometric Ratios and Functions 92 Lesson WWhat You Will Learnhat You Will Learn Draw angles in standard position Find coterminal angles Use radian measure Drawing Angles in Standard Position In this lesson, you will expand your study of angles to include angles
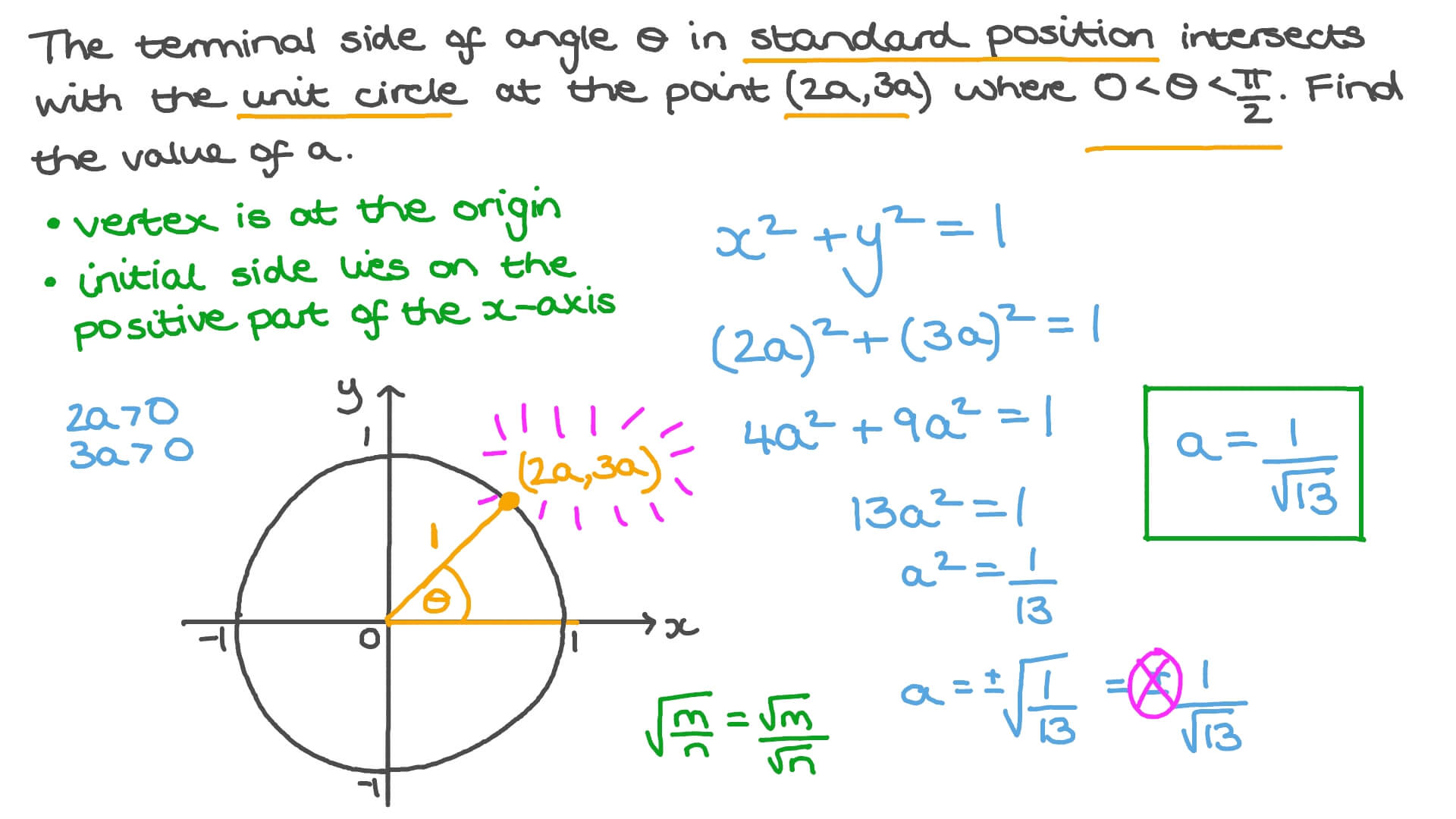


Question Video Using The Pythagorean Identities And Unit Circle To Solve An Equation In One Variable Nagwa



Radian And Degree Measure Ppt Download
PRACTICE Drawing Angles in Radians and Exact Values For each of the following a Draw the angle given in standard position b Find the related acute angle c Draw and label the special triangle d Use the triangle to state the trig ratios (primary on the left column, secondary on the right column) 1 3 4 π 2 4 3 π 3 6 π 4 5 3 π 5 5 4 πAn angle is in standard position when its vertex is at the origin 2 π °= radians All other special angles shown are multiples of theses angles Arc Length and Area of a Sector s and area A of a sector with radius r and central angle θ (measured in radians) are as followsQuadrantal Angle An angle in standard position whose terminal side lies along one of the axes Radian A unit of measure for angles 2Π radians equals one revolution and 360 degrees Ray A part of a line with a fixed endpoint on one end that extends without bound in


Pplato Flap Math 3 2 Polar Representation Of Complex Numbers



Radian And Degree Measure Ppt Download
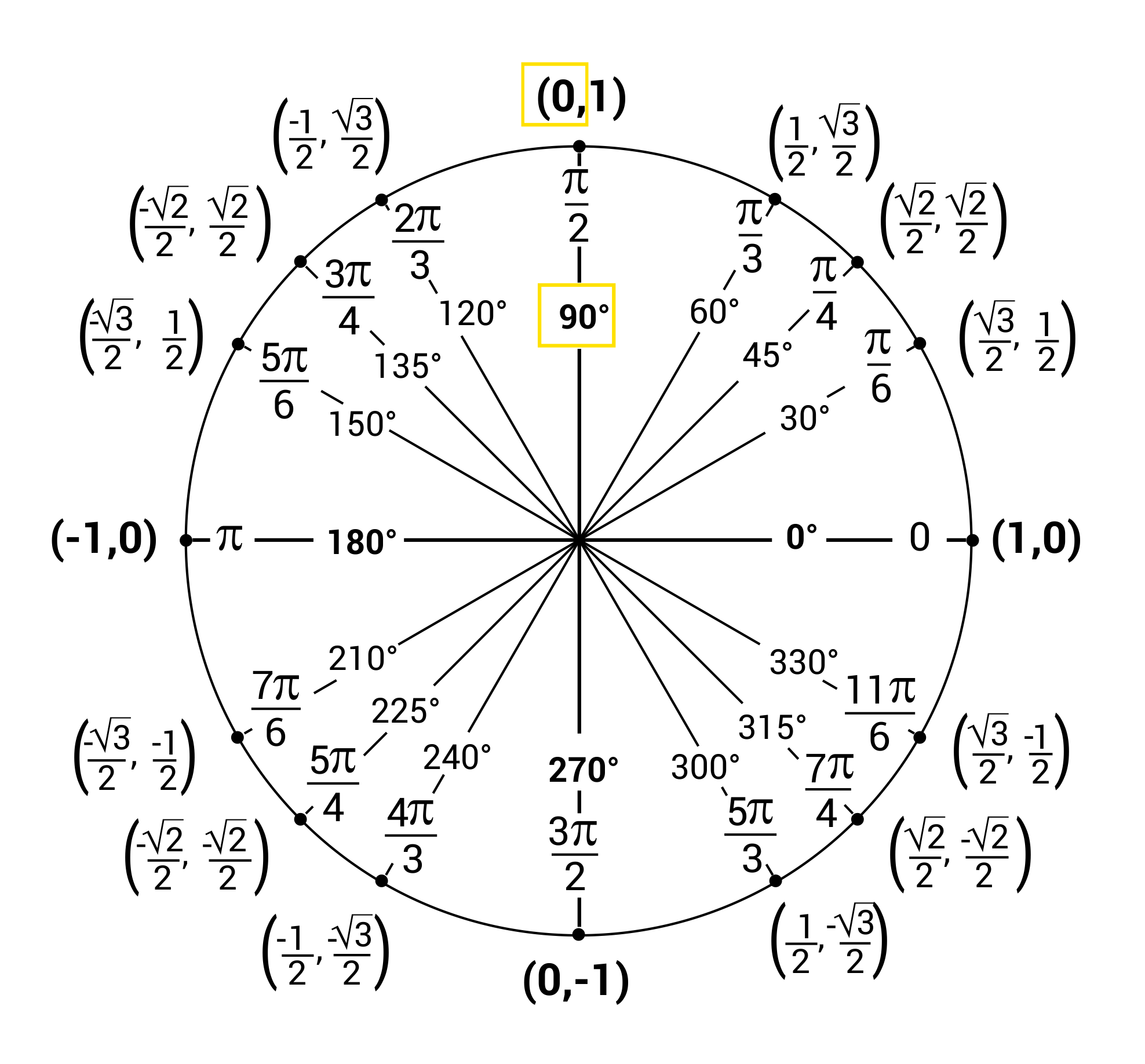
One half rotation is 180° or π radians One quarter rotation is 90° or π_ 2 radians One eighth rotation is 45° or π_ 4 radians Many mathematicians omit units for radian measures For example, 2_π 3 radians may be written as _2π 3 Angle measures without units are considered to be in radians Link the Ideas radian • one radian is theTrigonometric Ratios and Angle Measures Topics 1 Angle in standard position 2 Coterminal angles 3 Reference angle 4 Find the exact value of trigonometric ratios 5 ASTC rule in trigonometry (All Students Take Calculus) 6 Unit circle 7 Converting between degrees and radians 8 Trigonometric ratios of angles in radians 9 RadianCoterminal angles are angles in standard position (angles with the initial side on the positive x axis) that have a common terminal side For example 30 ° , − 330 ° and 390 ° are all coterminal To find a positive and a negative angle coterminal with a given angle, you can add and subtract 360 ° if the angle is measured in degrees or 2 π if the angle is measured in radians



Radian Angles Quadrants Video Radians Khan Academy



Day 9 Hw 1 And 2 Find A Coterminal Angle Between 0 And 2 Pi Youtube
(Through what quadrant does the terminal side pass when the angle is in standard position?) Solution Observe 3π 6 = π 2 < 5π 6 < 6π 6 =π , so 5π 6 is in Quadrant IIAngles Definition A quadrantal angle is an angle in standard position whose terminal ray lies along one of the axes Examples of quadrantal angles include, 0, π/2, π, and 3π/ 2Oct 13, 11 · Draw an angle with the given measure in standard position 1) 110o 2) 450o 3) 3π/2 (Hint change to degrees first) Find one positive angle and one negative angle that are coterminal with the given angles 4) 87o 5) 1o Apr 71250 PM 6) Let (3,4) be a point on the terminal side of an angle θ in standard position
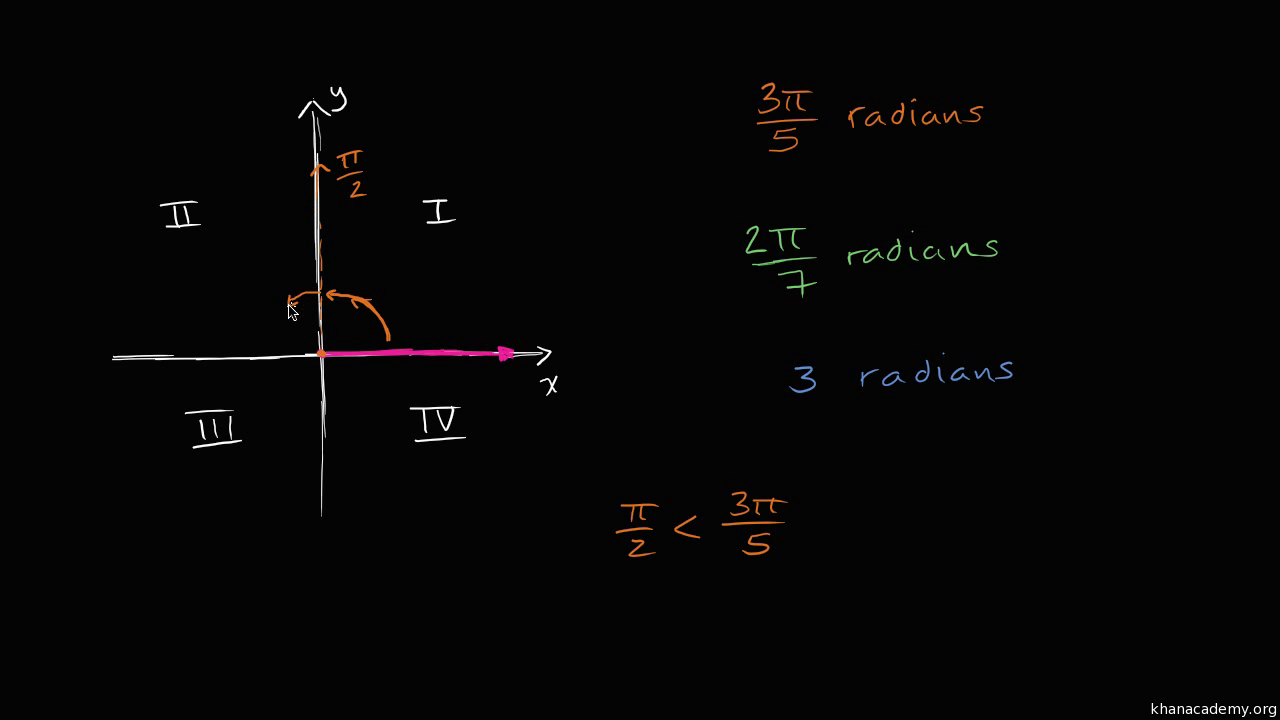


Radian Angles Quadrants Video Radians Khan Academy
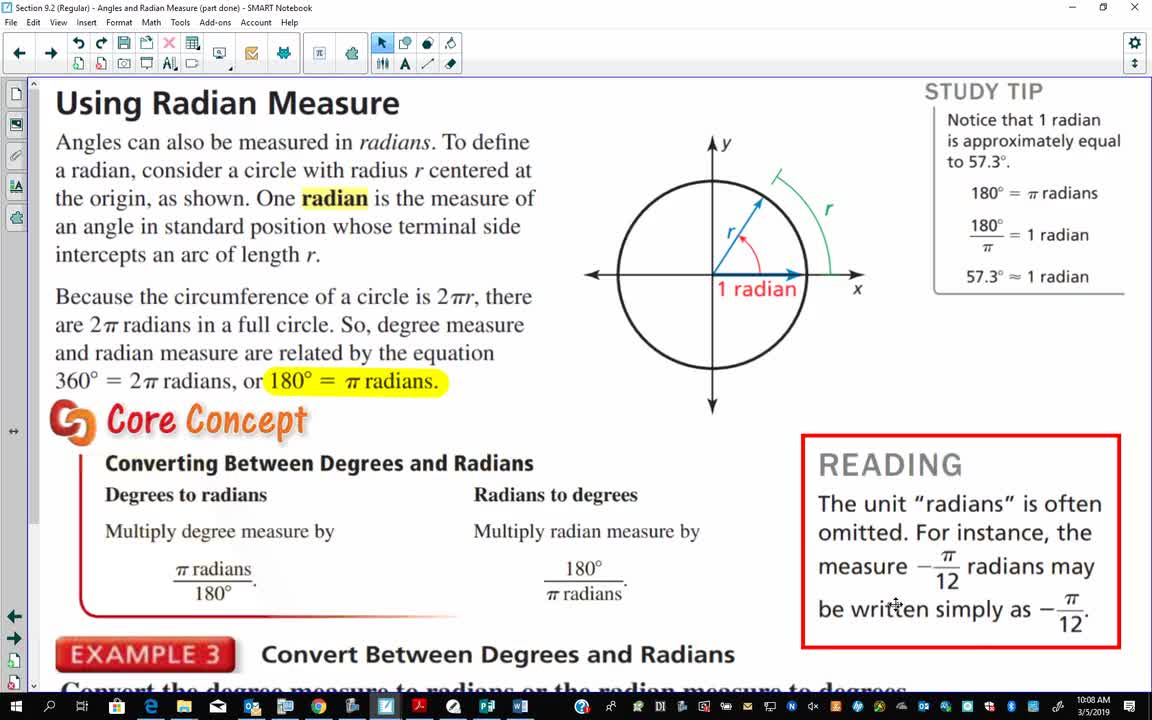


Regular Algebra 2 Section 9 2 Part 2 21 Minutes Yankton High School
Solution for (a) Draw the angle in standard position (b) Convert to radian measure using exact values rad (c) Name the reference angle in both876 ft To find the area, use the area formula, but remember to use radians, 2 π 3, instead of the degrees, 1°2 48 π π The angle 3 4 π α is 3 8 of a full rotation in the counterclockwise direction 5b Draw the angle 7 6 π α in standard position 5c Draw the angle 13 4 π γ in standard position Since the angle is positive, it is obtained by a counterclockwise rotation Express the angle as a fractional part of 2π 13 13 2 48 π π The angle


Pre Calculus Story Board Project Kuvakasikirjoitus By Vanessatannetta



Math 30 1 Degrees And Radians
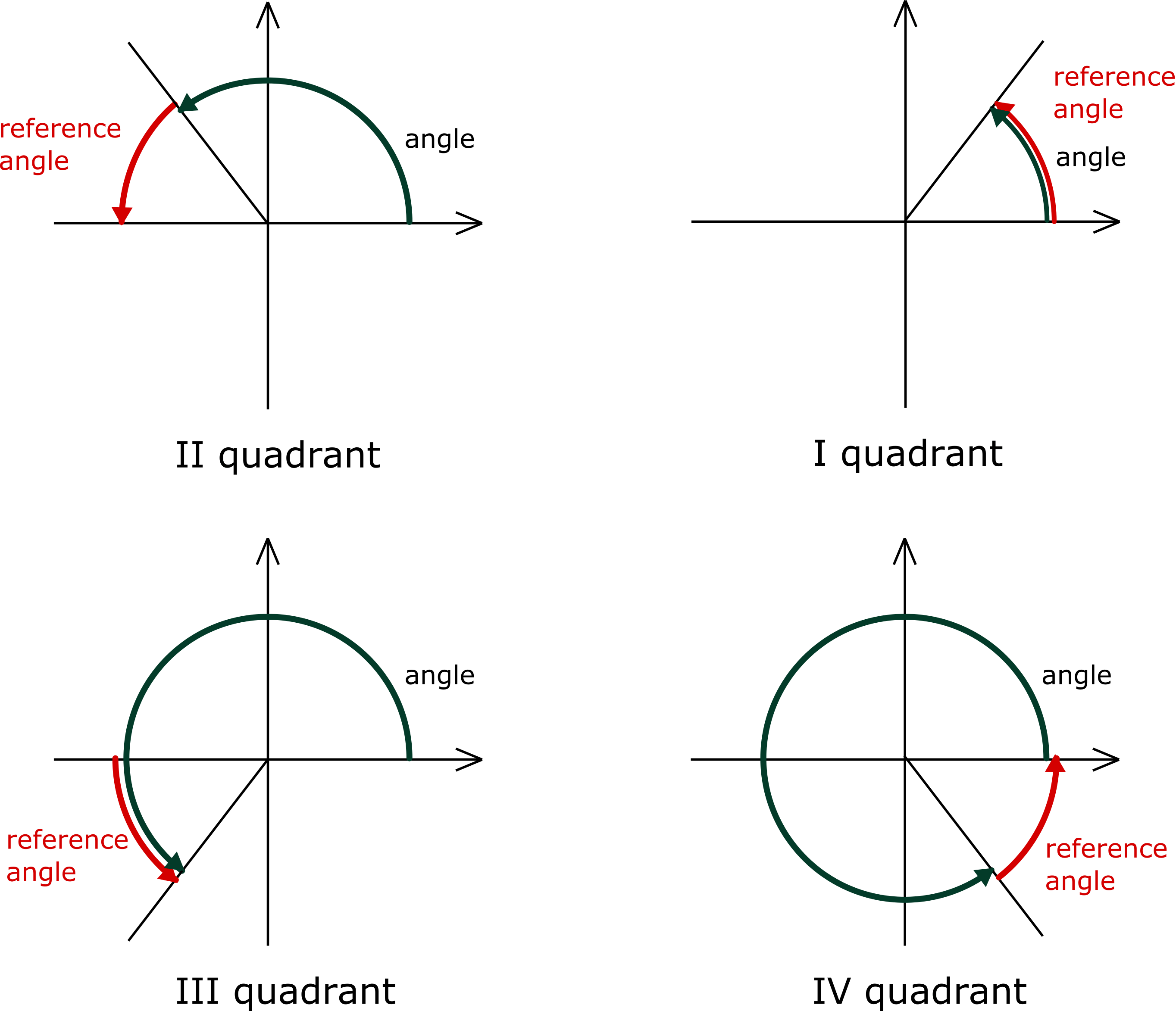
First convert to radians 4 45 π °= And so with 4 π θ= we have ( ) 2 2 4 4 2 π π = ⋅ A = Problems 8 Find the area of a sector determined by a 196° angle in a circle of radius 6 9 Find the area of a sector determined by 3 5π radians in a circle of radius 2 THE TRIGONOMETRIC FUCTIONS For an angle θ in standard position, letInclude an explanation of 1 radian in your paragraph 5 Explain the differences between linear speed and angular speed when describing motion along a circular path For the following exercises, draw an angle in standard position with the given measure 6 30° 7 300° 8Dec 28, 16 · 0 to π/2 first quadrant, so reference angle = angle, π/2 to π second quadrant, so reference angle = π angle, π to 3π/2 third quadrant, so reference angle = angle π, 3π/2 to 2π fourth quadrant, so reference angle = 2π angle 10π/9 is a bit more than π


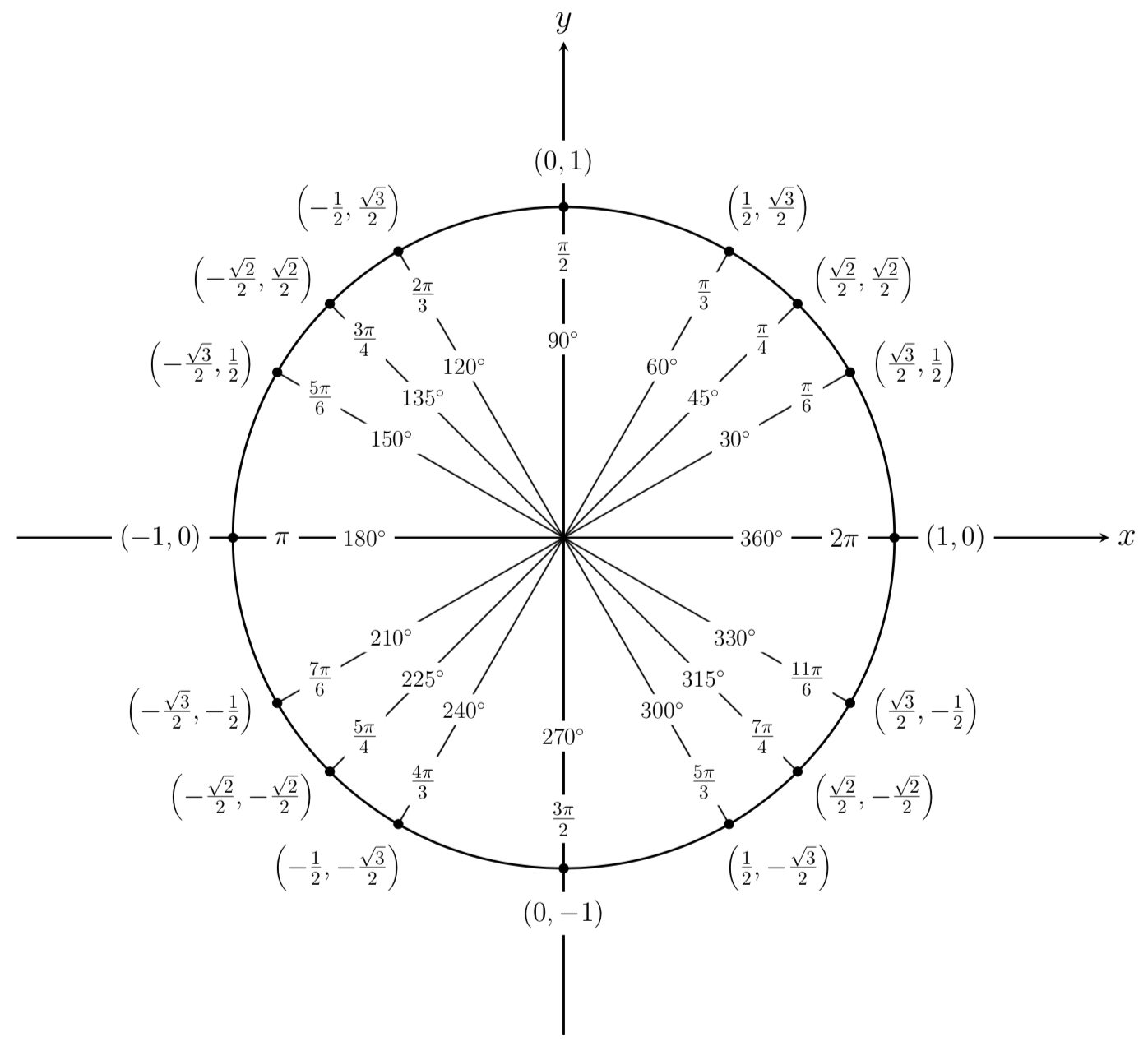
Unit Circle Calculator Inch Calculator
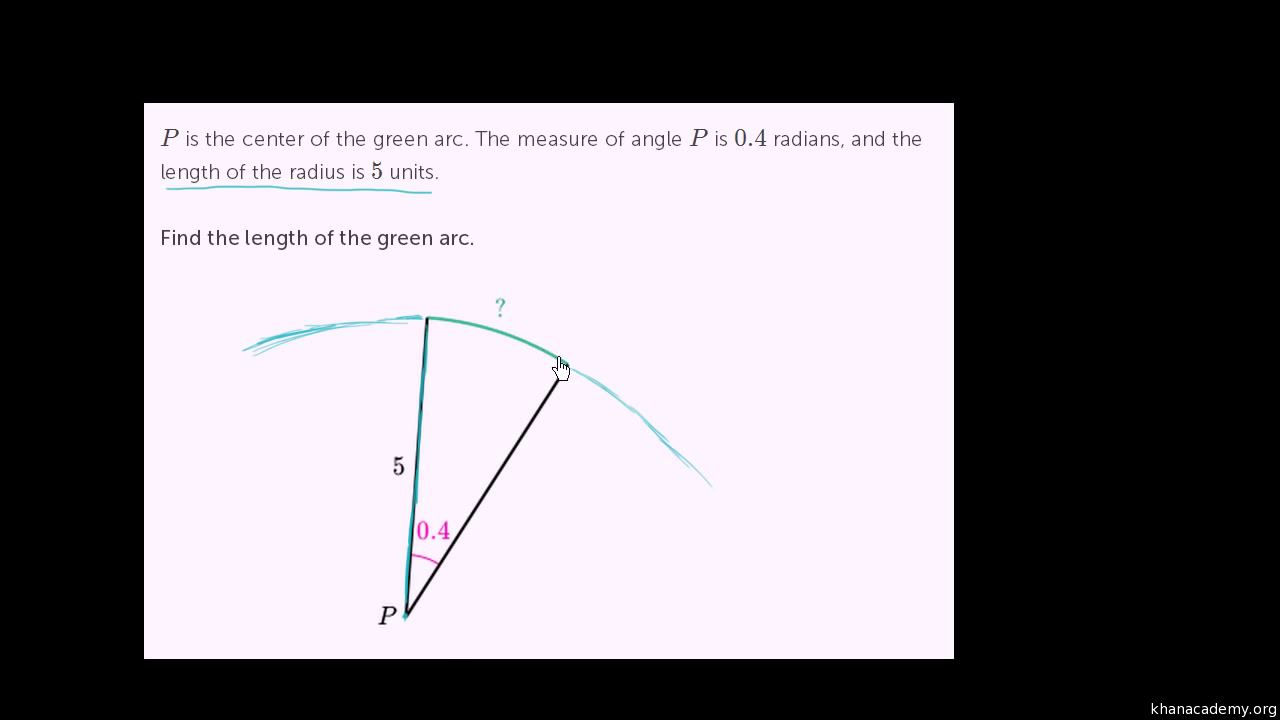


Arc Length From Subtended Angle Radians Video Khan Academy
Nov 22, 17 · Let's draw an angle in standard position that measures 2π/3 radians First, let's convert 2π/3 to degrees Remember, 360° = 2π radians, and converting means multiplying by 360°/2π or 2π/360Apr 05, 18 · Objective Sketch the angle #((23pi)/3)# in the standard position An angle is said to be in the standard position in the Cartesian Coordinate System if it's vertex is at the origin and it's initial side lies on the positive xaxis #color(green)("Step 1")# Examine the image (this was originally constructed using a computer software) given below with the angles measured in radians4) Two or more angles in standard position with the same terminal side are called coterminal angles Add or subtract the multiple of 360 ˚ to given angle to find its coterminal angles *We can draw any angle measures from −∞ to ∞ in standard position The term general angle is used to indicate that these angles are not restricted



Sketch The Angle In Standard Position Youtube



Find The Degree Measure Corresponding To Following Radian Measures
Radian angles & quadrants Google Classroom Facebook Twitter Email Radians that is going to get us to PI over 2 so that would have been PI a rotation a counterclockwise rotation of PI over 2 radians now it's 3 PI over 5 greater or less than that well 3 PI over 5 3 PI over 5 is greater than or I guess in other word could say it is 3 PIThis question is asking arc length In order to used the arc length formula, the angle needs to be in radians 1 ° π 180 ° = 2 π 3 Now use the arc length formula s = r θ s = 400 ft 2 π 3 s = 800 π 3 ft ≈2 π radians = 360° π radians = 360° 2 = 180° 1 radian = 180° π ≈ 573° 2 π radians = 360° π radians = 360° 2 = 180° 1 radian = 180° π ≈ 573° See Figure 11 Note that when an angle is described without a specific unit, it refers to radian measure
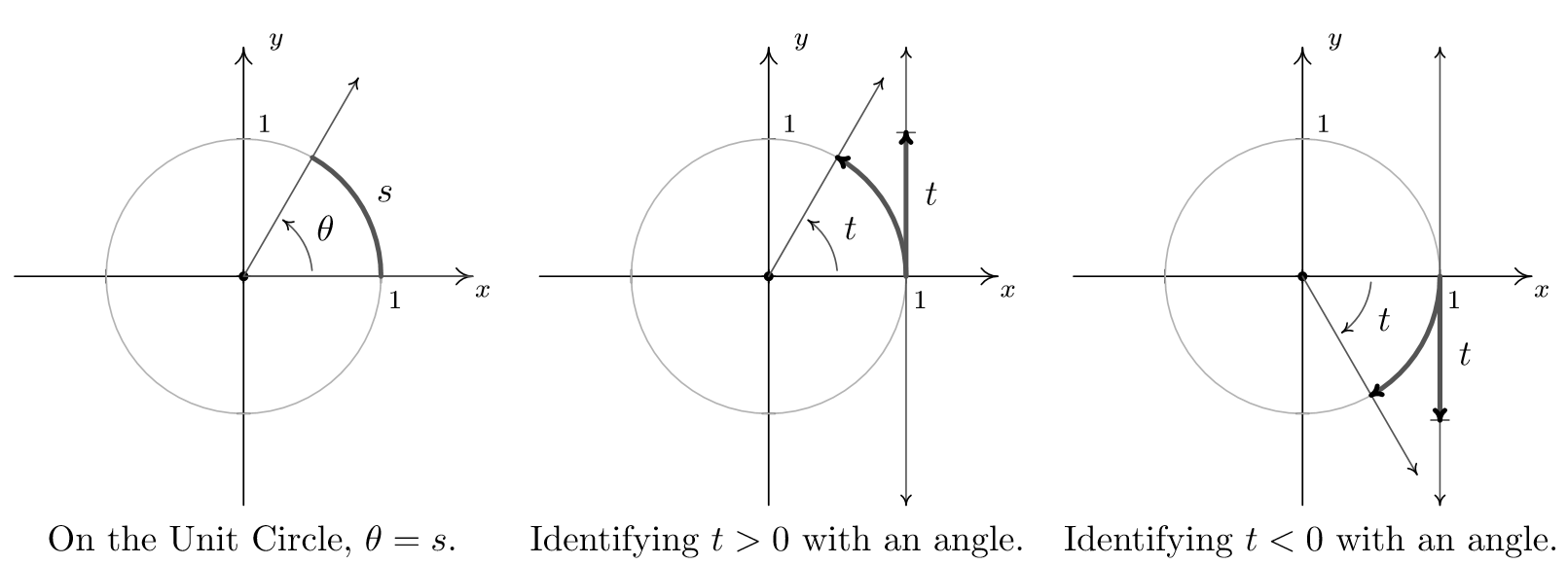


10 2 Angles And Their Measure Mathematics Libretexts


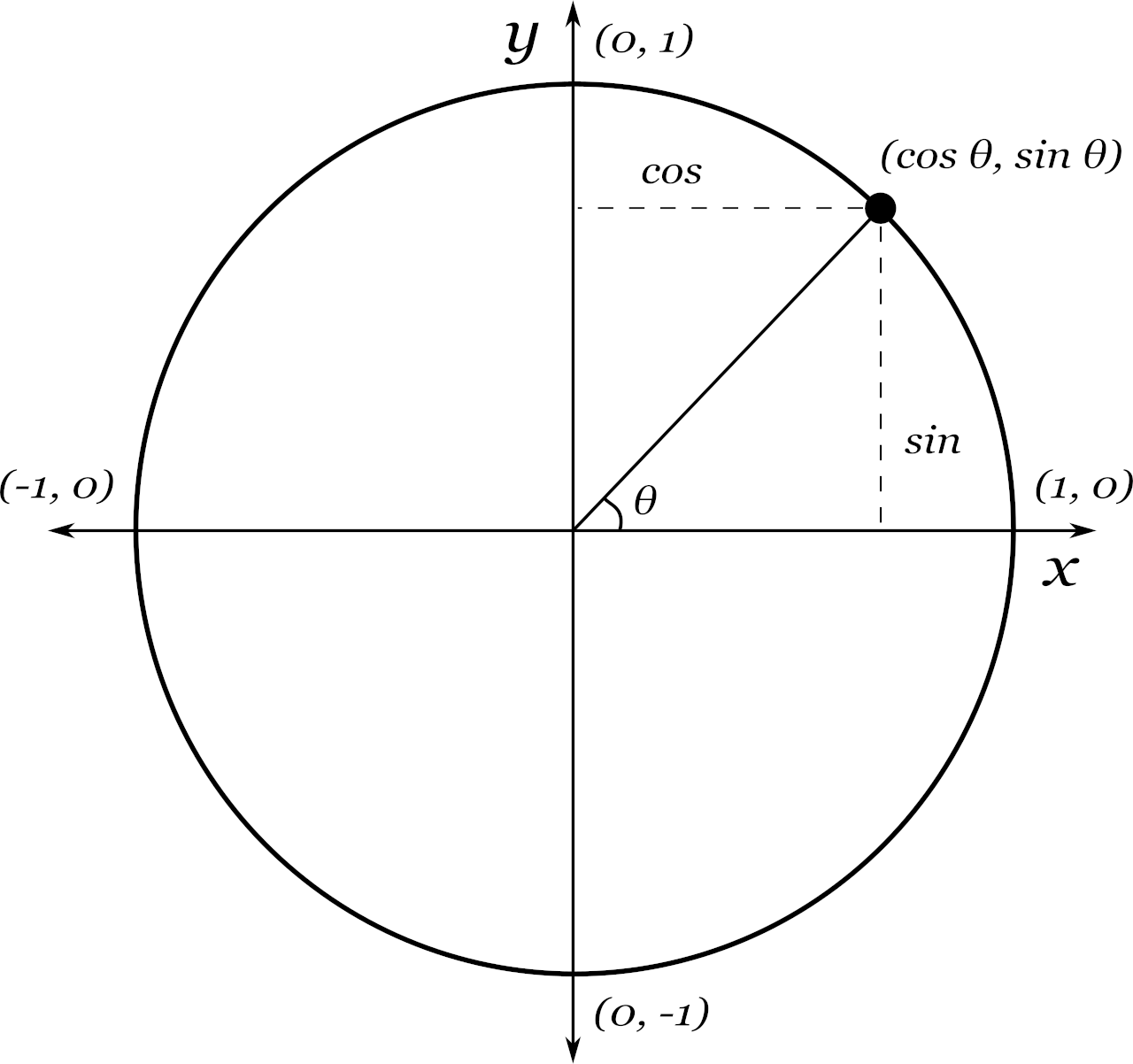
What Is The Unit Circle Expii
Example Convert each angle in radians to degrees a 2 b c 3 5 d 6 2 e 3 π π π π πDrawing Angles in Standard Position Angles Formed by Revolution of Terminal Sides Example Draw and label each angle in standard position 3 a 2 bAnd radian measures of special angles in the first quadrant and for 90 2 π °= radians All other special angles shown are multiples of theses angles Arc Length and Area of a Sector The arc length s and area A of a sector with radius r and central angle θ (measured in radians) are as follows Arc length s = rθ Area 2 1 2 A = r θ Notes 0° 0 x y 360° 2 45°Angles in Standard Position Practice Problems I Relationship Between Degrees and Radians Angles are measured in either degrees or radians (rad) One complete revolution, which is 360 , equals 2π rad So 360 =2π rad, or 180 = π rad This means 1 = π 180 rad and 1 rad= 180 π To change from degrees to radians, multiply by π



Angles Precalculus Ii
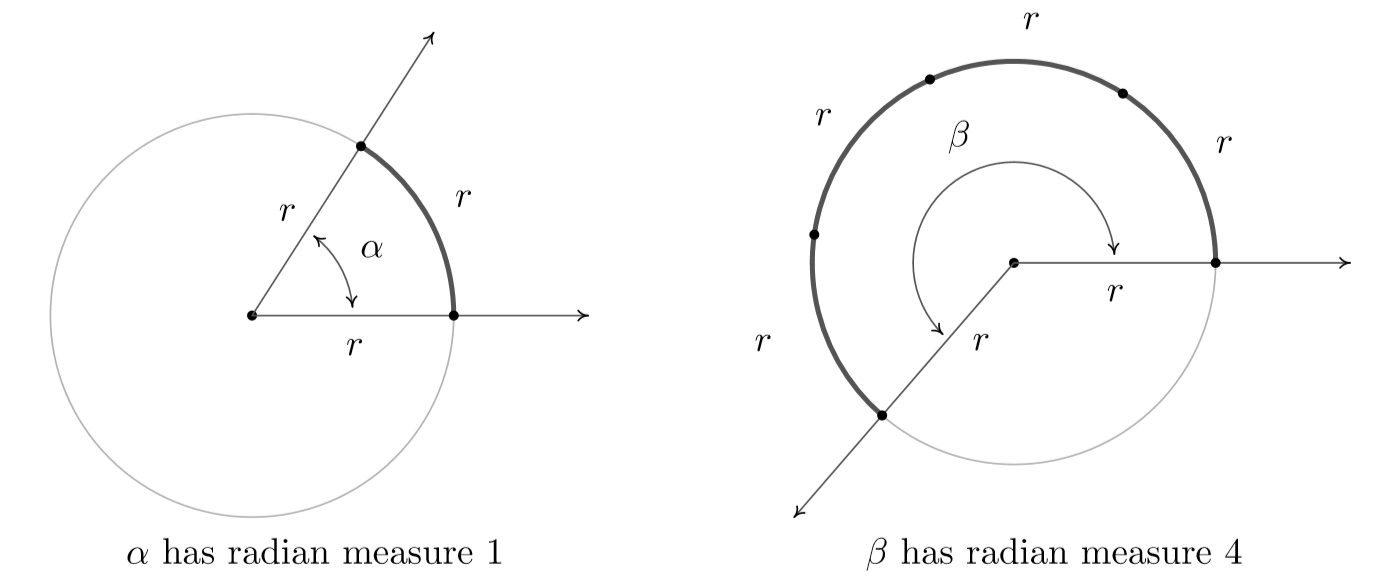


10 2 Angles And Their Measure Mathematics Libretexts
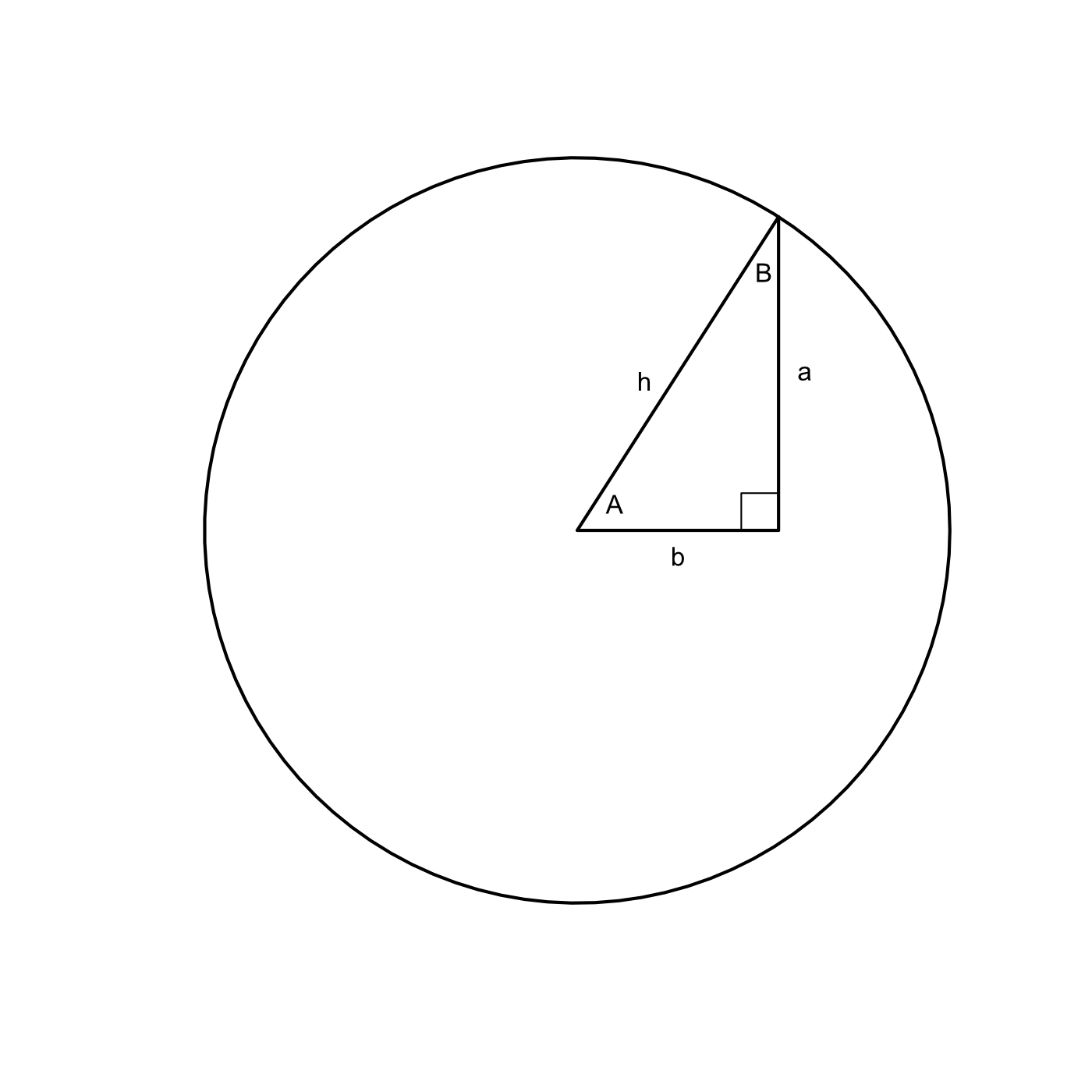
Area of a Sector of a Circle For a circle of radius r, the area A of a sector of the circle with central angle θ is given by 1 2 2 ArT where θ is measured in radians Examples Find the area of the sector of the circle with radius r and central angle θ 1 r = 6 inches, θ = π/3 2 r = 25 feet, θ = 225A The angle in standard position formed by rotating the terminal side of an angle one complete counterclockwise rotation has a radian measure of π radians B The angle in standard position formed by rotating the terminal side of an angle one complete counterclockwise rotation has a measure of 360 degrees Cπ 2 radians The quadrants and some quadrantal angles (For convenience, we may label a standard angle by labeling its terminal side) Example What quadrant does 5π 6 lie in?
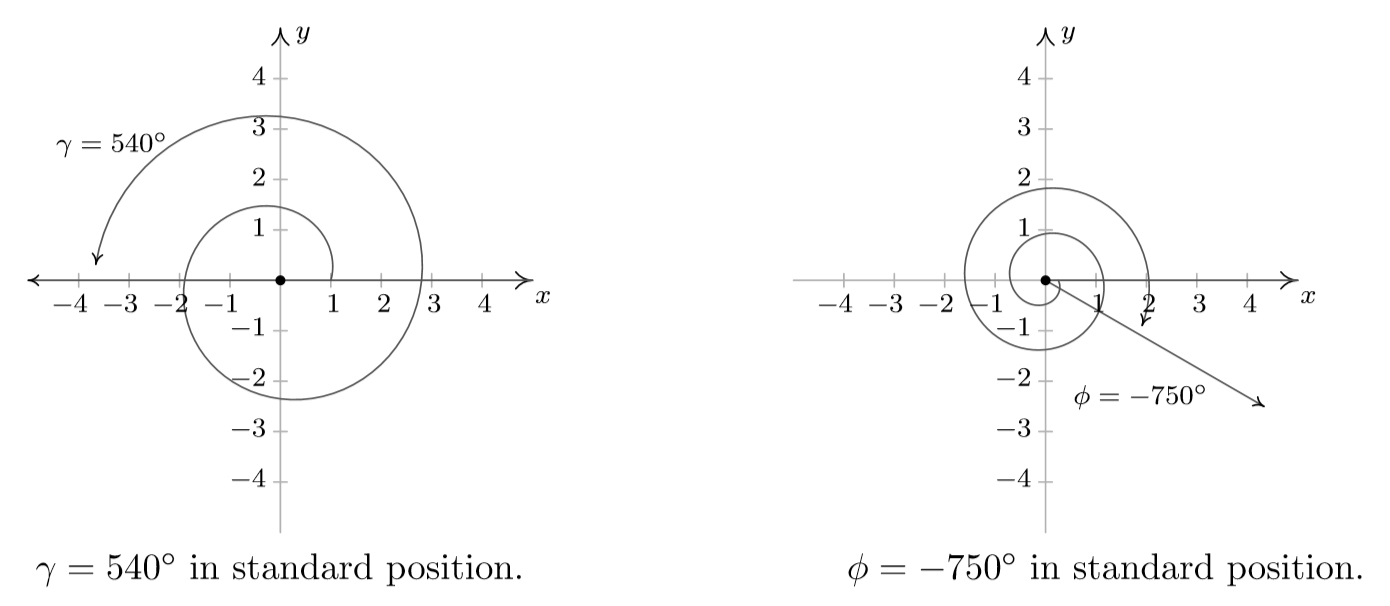


10 2 Angles And Their Measure Mathematics Libretexts
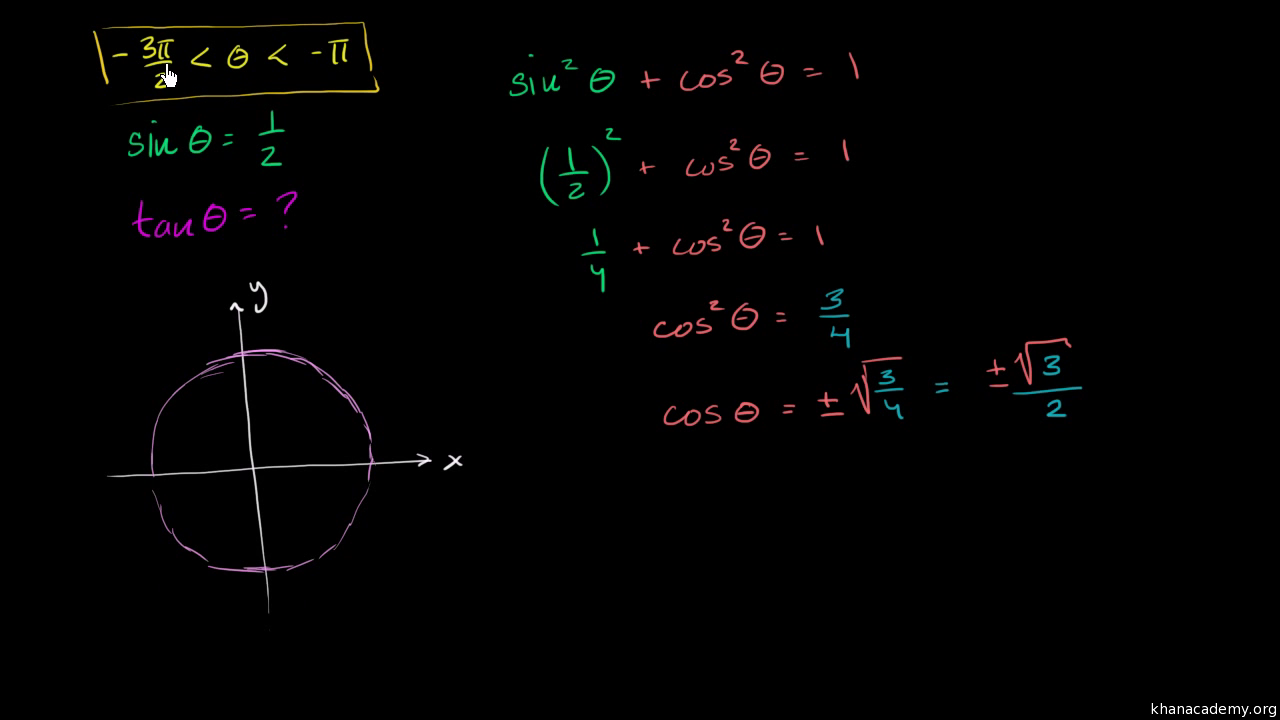


Using The Pythagorean Trig Identity Video Khan Academy
Assume that α is an angle in standard position whose terminal side contains the given point and that 0 α π/2 Find the radian measure of α to the nearest tenth of a radian Stepbystep solutionQuadrantal Angles (Radian Family) 0, π/2, 2π/2, 3π/2, 2π Standard Position Angles sketched in standard position always place the vertex on the (origin) and the intial ray on the (xaxis) Standard PositionSame locationStandard Position of Angles Degrees and Radians DRAFT 3 years ago by moconno2 9th 12th grade Mathematics 1/2 π 1 π alternatives 2π 1/2 π Q angle in standard position with teminal ray on an axis answer choices quadrantal angle


Solved Find The Degree Measure Of The Angle With The Give Chegg Com



Steradian Wikipedia
Jan 04, 16 · region bounded by 2 radii and an arc of a circle Area #, of a sector of a circle with radius N, and central angle à, measured in radians is 1 Find the area of a sector of a circle with a central angle measuring 8 radians and a radius of 12" 1 2 2 A r 1 12 18 5655 2 2 24 AinAnswer choices top left top right bottom s Question 10



Unit Circle Sine And Cosine Functions Precalculus Ii


Mathematical Investigation A Level Maths Marked By Teachers Com



Write The Expression In Simplest Form Ppt Download



Algebra 2 Section 9 2 28 Minutes Yankton High School



Find The Degree Measures Corresponding To The Following Radian Me



T1 1d To Find Coterminal Angles Ppt Download



Radian And Degree Measure



T1 1c Define Radians Convert Between Radians And Degrees Ppt Download


Intuitor Getting A Grip On Statistics Science And Philosophy


Mfg The Unit Circle



Math Teacher Mambo Unit Circle And Radians



Radians And Degrees Youtube



Position Angle Wikipedia



Trigonometric Functions


Question No 2 Conversion Of Radian Into Degrees Video Dailymotion



How To Find The Reference Angle In Radians And Degrees Trigonometry Youtube



What Is The Unit Circle Expii



Trigonometry And Applications Ppt Download



Archimedes Radians Pi Page 1 Line 17qq Com



Cos Pi 2 In Radians Page 1 Line 17qq Com



Section 3 1 Radians And Angles In Standard Position Ppt Download



Section 4 1 Radian And Degree Measure 1 Drawing Angles In Standard Position


Mfg The Unit Circle
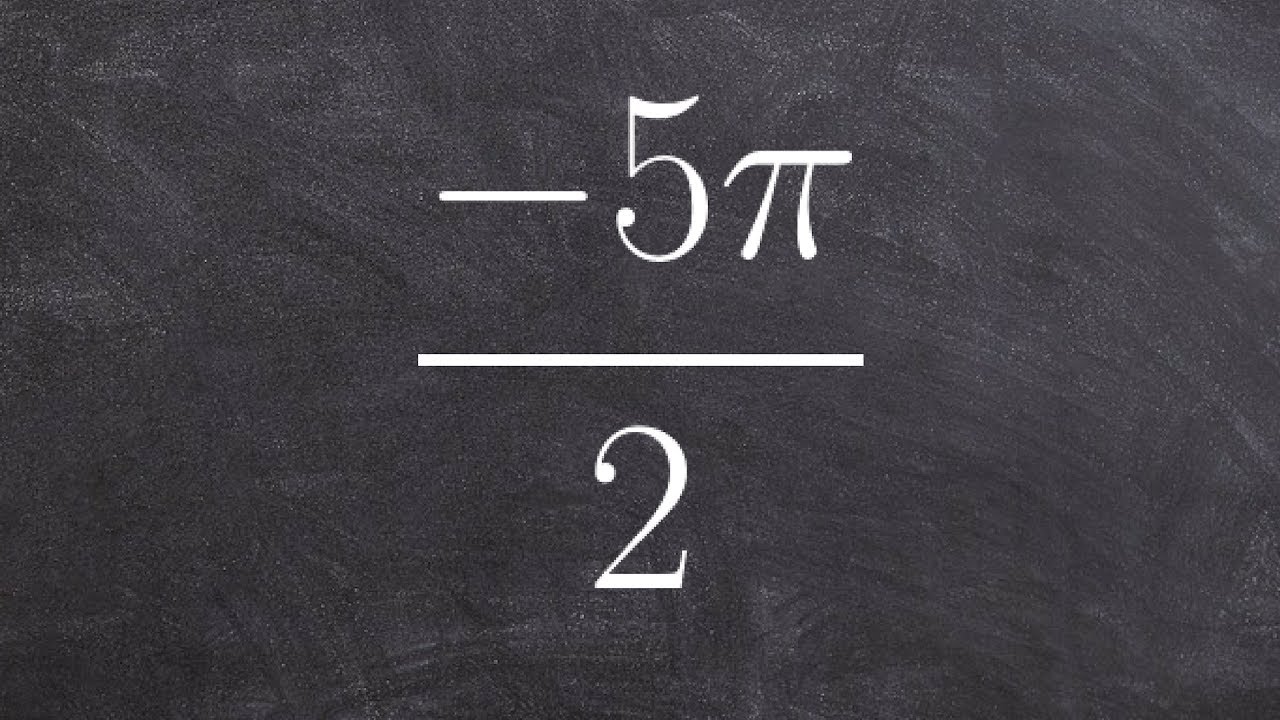


Sketch The Angle In Standard Position Youtube



Angles Precalculus Ii
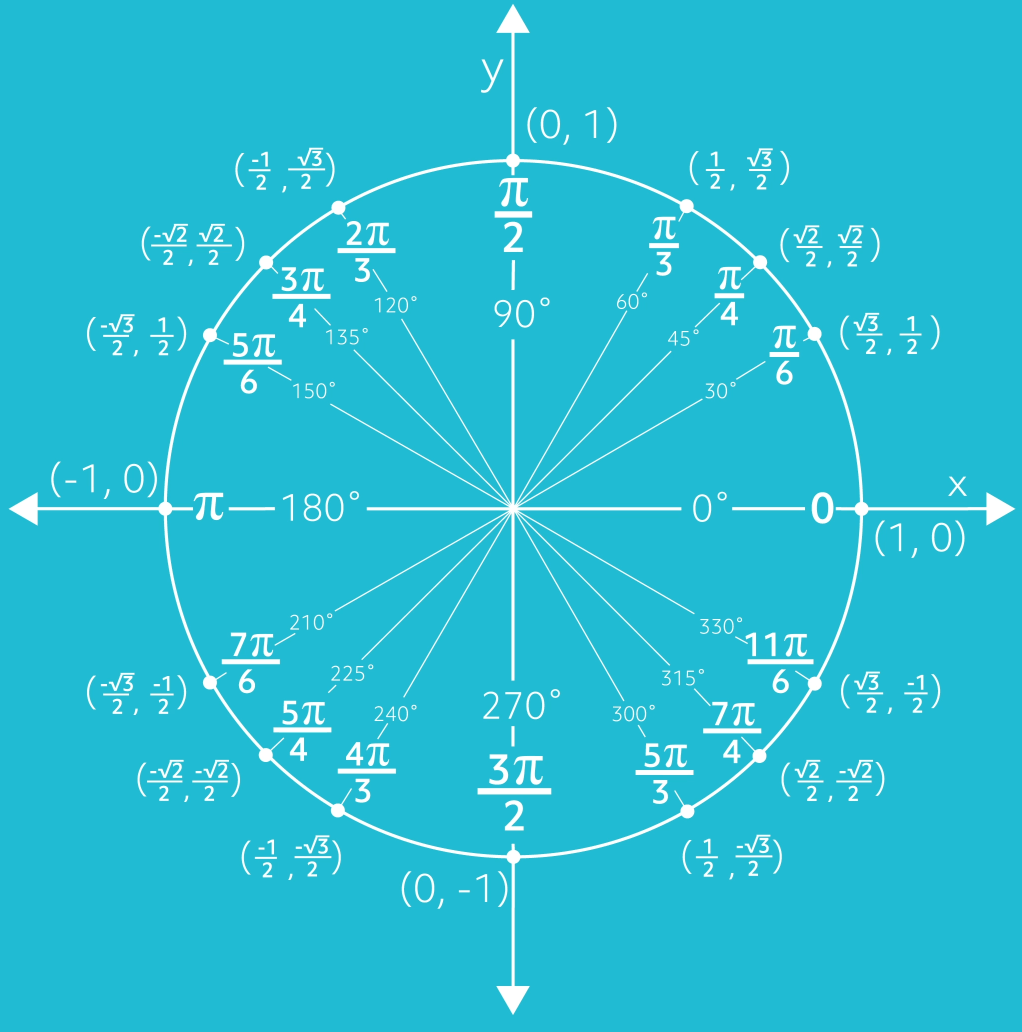


Unit Circles And Standard Position Video


Mfg The Unit Circle


If You Teach Trig You Need This Post Insert Clever Math Pun Here



Subdivide The Unit Circle By Pi 6 And Pi 2 Youtube
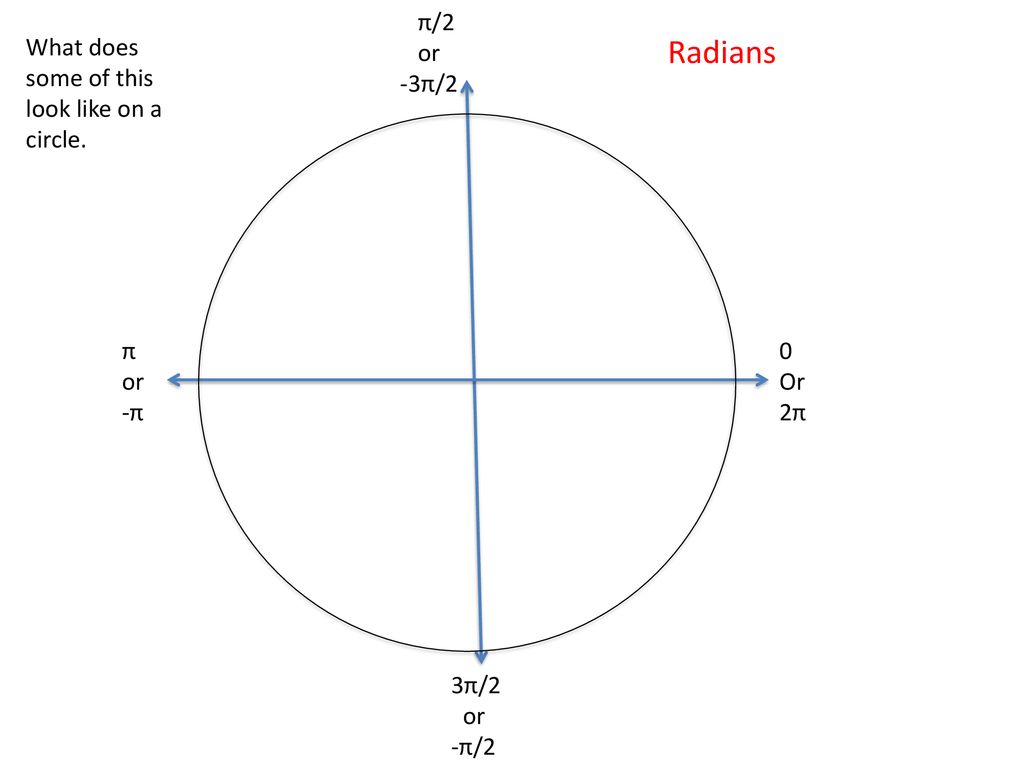


Terms To Know Going Forward Ppt Download



2 Pi Radians Page 1 Line 17qq Com


Webpage Of Dr Tom Cuchta



Radian And Degree Measure Ppt Download



Sketch The Angle In Radians In Standard Position Youtube



Examples Determining Coterminal Angles In Radian Measure Youtube



Angles Arc Lengths And Trig Functions Basic Example Video Khan Academy



Angles Precalculus Ii


Reference Angle Calculator Definition Graph Quadrants



Radian And Degree Measure Ppt Download


Pplato Flap Math 1 6 Trigonometric Functions



Sine And Cosine Values In Radians Using Reference Triangles Multiplies Of Pi 6 And Pi 3 Youtube



Exam 2 Review Key



2 Pi Radians Page 1 Line 17qq Com



Sine Wikipedia


Unit Circles And Standard Position Video


Find The Reference Angle For 8 Pi Divided By 5 Socratic



Ppt 2 1 Degrees And Radians Powerpoint Presentation Free Download Id
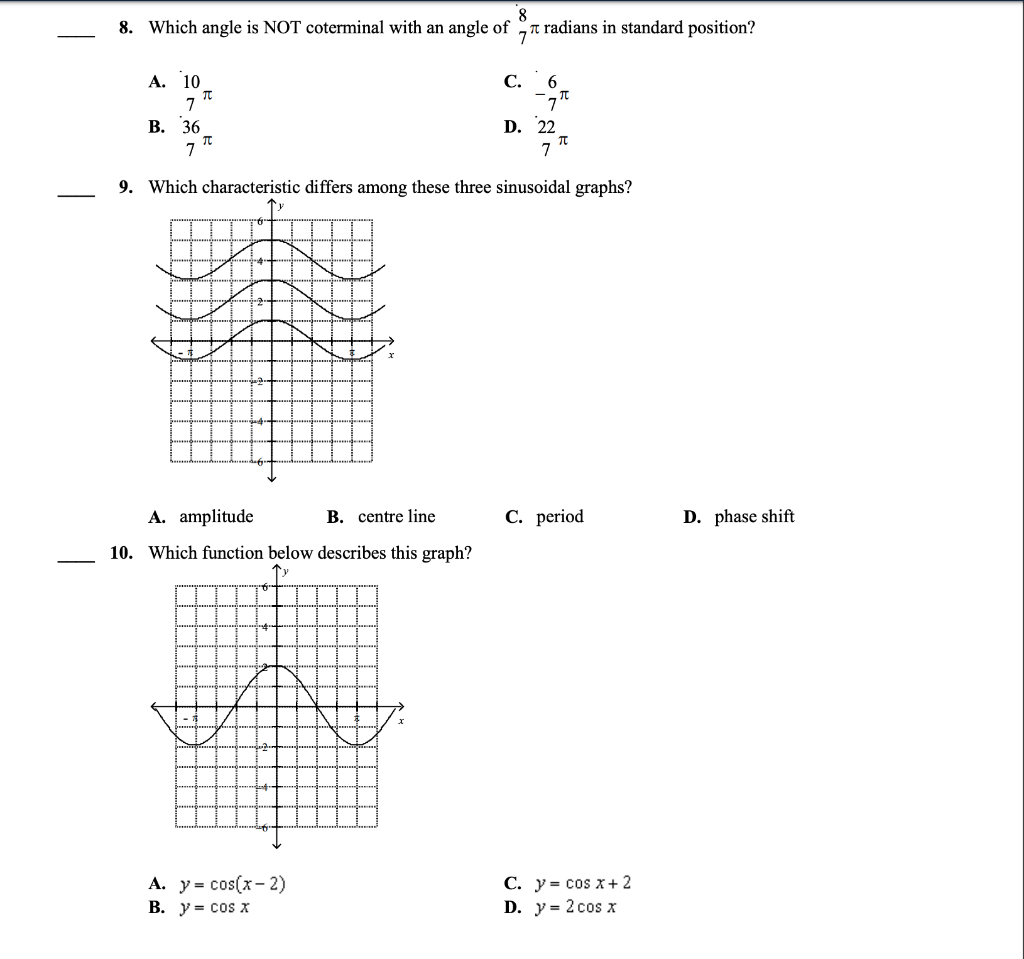


Solved 8 8 Which Angle Is Not Coterminal With An Angle O Chegg Com



Ppt 9 2 Define General Angles And Use Radian Measure Powerpoint Presentation Id


Mfg Polar Coordinates



Angles Precalculus Ii



Objectives After Completing This Section You Should Be Able To Pdf Free Download



Let Theta Be A Positive Angle If The Number Of Degrees In Thet



Trigonometric Functions Ppt Video Online Download



Degrees To Radians Video Trigonometry Khan Academy



Day 9 Hw 1 And 2 Find A Coterminal Angle Between 0 And 2 Pi Youtube



Measure Center Angle In Radians Page 1 Line 17qq Com



Radian Measure Arc Length And Circular Motion Ppt Download



How Do You Find The Sine Cosine And Tangent Of 19pi 2 Radians Socratic


